Аффинное оценивание элементарных функций

Для эффективного и широкого применения рассмотренных выше алгоритмов нужно уметь находить интервальные и аффинные оценки всех входящих в целевую функцию элементарных функций. В то время как задача получения интервальных оценок хорошо изучена и проста в реализации на вычислительном устройстве, аффинное оценивание является процессом значительно более сложным и мало изученным [5]. Автором данной работы были детально исследованы и усовершенствованы способы аффинного оценивания функций, и разработаны соответствующие алгоритмы. Некоторые результаты этого исследования мы рассмотрим ниже.

Как уже было сказано, чтобы оценить формулу в AA мы должны заменить каждую из элементарных операций z = ¦(x, y) на вещественных числах эквивалентной операцией 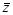= 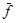(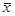, 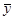) над аффинными формами [4,7], где  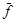- процедура, вычисляющая аффинную форму z = ¦(x, y), которая соответствует , .

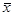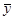По определению

x = x ₀ + x ₁e₁ + … + x _ne_n    (1)

y = y ₀ + y ₁e₁ + …+ y _ne_n    (2)

для некоторых (неизвестных) значений (e₁, …, e_n)ÎUⁿ, где Uⁿ есть декартово произведение n вещественных интервалов [-1, 1]. Поэтому величина z есть функция e_i, а именно

z = ¦(x, y) = ¦(x ₀ + x ₁e₁ + … + x _ne_n, y ₀ + y ₁e₁ + …+ y _ne_n) = ¦*(e₁,…,e_n) (3)

Процедура 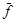 теперь должна заменить ¦*(e₁,…,e_n) аффинной формой

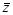 = z ₀ + z ₁e₁ + …+ z _ne_n,

которая сохраняет столько информации, сколько возможно из соотношений между x, y и z, вытекающих из (1-3), но без использования других ограничений, которые не могут быть выведены из начальных данных.

В общем случае, когда ¦ является нелинейной операцией, функция ¦*(e₁,…,e_n) = ¦(x, y) из (3) не может быть выражена как линейная комбинация e_i. В этом случае мы можем подобрать некоторую линейную функцию

¦^a(e₁,…,e_n) = z ₀ + z ₁e₁ + …+ z _ne_n, (4)

которая аппроксимирует ¦*(e₁,…,e_n) равномерно на области Uⁿ, и затем добавить к ней дополнительный член z _ke_k, представляющий ошибку аппроксимации. Таким образом,

z = ¦^a(e₁,…,e_n) + z _ke_k = z ₀ + z ₁e₁ + …+ z _ne_n + z _ke_k.

Здесь e_k должен быть новым символом шума (отличным от всех других символов шума в одном вычислении) и величина z _k должна быть верхней границей модуля разницы между ¦^a и ¦* для всех возможных значений e₁,…,e_n; т.е.

max { | ¦*(e₁,…,e_n) - ¦^a(e₁,…,e_n) |: (e₁,…,e_n)ÎUⁿ }

Заметим, что замена ¦* на ¦^a + z _ke_k частично отходит от основной цели AA: символ шума e_k принимается независимым от e₁,…,e_n, в то время как фактически это функция от них. Любые последующие операции, использующие z в качестве входного значения, не имеют сведений о взаимосвязи между e_k и e₁,…,e_n и поэтому могут возвращать аффинную форму, которая менее точна, чем необходимо.

Для минимизации потерянной информации мы должны выбрать коэффициенты z ₀, z ₁,…, z _n таким образом, чтобы сделать новый член ошибки как можно меньше.

Другими словами ¦^a должна быть многочленом первой степени, который наилучшим образом аппроксимирует ¦* на Uⁿ в смысле Чебышева минимизации максимальной ошибки.

Отметим одно свойство, которое окажется нам полезным в дальнейшем. Пусть нам надо найти наилучшую линейную аппроксимацию для функции ¦(x (e₁,…,e_n)), где x (e₁,…,e_n) = x ₀ + x ₁e₁ + … + x _ne_n, тогда ¦*(e₁,…,e_n) = ¦(x ₀ + x ₁e₁ + … + x _ne_n) аппроксимируется на гиперкубе Uⁿ некоторой функцией ¦^a(e₁,…,e_n) = z ₀ + z ₁e₁ + …+ z _ne_n. Заметим, что функция ¦*(e₁,…,e_n) – константа на любой гиперплоскости из Uⁿ, ортогональной вектору (x ₁,…, x _n). Нетрудно показать, что наилучшая (по Чебышеву) линейная аппроксимация ¦* также должна обладать этим свойством. Т.е. нам нужно рассматривать только аппроксимации ¦^a(e₁,…,e_n) вида

¦^a(e₁,…,e_n) = a 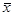 + b = a(x ₀ + x ₁e₁ + … + x _ne_n) + b.

Также легко показать, что значения a и b, которые минимизируют максимальную ошибку ¦^a – ¦* есть в точности коэффициенты наилучшей линейной аппроксимации функции ¦(t) функцией a t + b на интервале [ 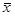]. Таким образом, задача аппроксимации исходной функции n переменных редуцируется в задачу аппроксимации функции одной переменной. Можно показать (см. [16]), что для функции одной переменной прямая a t + b будет наилучшей линейной аппроксимацией на отрезке [ a, b ], если

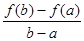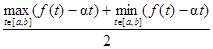a = , b = (5)

 Далее мы построим линейное приближение для конкретных функций: 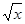и e^x. Техника, иллюстрируемая этими примерами, может быть легко распространена на большинство других элементарных операций и функций.

Аффинная оценка функции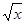

Итак, рассмотрим аффинную оценку функции 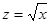 [8]. Нам нужно аппроксимировать функцию ¦*(e₁,…,e_n) = 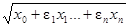на гиперкубе Uⁿ некоторой функцией ¦^a(e₁,…,e_n) = z ₀ + z ₁e₁ + …+ z _ne_n и затем добавить к последней дополнительный член z _ke_k для учета ошибки аппроксимации, где e_k вновь созданный символ шума.

Как показано ранее, нам нужно рассматривать только аппроксимации вида ¦^a(e₁,…,e_n) = a 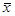 + b = a(x ₀ + x ₁e₁ + … + x _ne_n) + b.

Если [ a, b ] – интервал [ 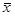], то оптимальные чебышевские коэффициенты a и b есть

a =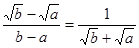

b =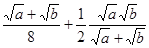

и максимальная ошибка аппроксимации d =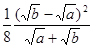

Эта ошибка возникает на границах интервала, где кривая лежит ниже аппроксимирующей прямой и в точке c = 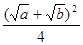, где кривая расположена выше прямой.

После того как a, b и d получены, мы можем вычислить

z ₀ = a x ₀ + b

z _i = a x _i     (i = 1,…,n)

z _k = d

Этот анализ подразумевает, что мы можем вычислить a, b и d точно. На практике же, вычисление a может выйти за пределы машинно-представимых чисел с плавающей точкой и, таким образом, мы получим только приближение a¢ к оптимальному наклону a. Затем мы должны выбрать b так, чтобы минимизировать максимум |a¢ x + b - 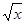| вместо |a x + b - 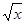|. И опять мы сможем только вычислить приближение b¢ к оптимальному b. Ошибка аппроксимации d тогда будет максимумом |a¢ x + b¢ - 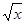|; и снова мы способны вычислить только верхнюю границу d¢ для нее.

После этого формулы для расчета z _i должны быть изменены для использования a¢, b¢ и d¢ вместо a, b и d. В действительности, вычисление z ₀, z ₁,…, z _n по этим формулам будет ухудшено ошибкой округления; поэтому мы должны будем определить верхние границы d¢₀, d¢₁,…, d¢_n для этих ошибок и добавить их к ошибке аппроксимации d¢, всегда округляемой вверх, для получения ошибочного члена z _k.

Аффинная оценка функции e ^x

Найдем линейную аппроксимацию ¦^a(e₁,…,e_n) = z ₀ + z ₁e₁ + …+ z _ne_n для функции ¦(x) = e^x. Пусть a, b и d имеют тот же смысл, что и в предыдущей части, [ 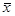] = [ a, b ]. Тогда из (5) следует, что a = 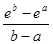. Для вычисления b нам нужно знать максимум и минимум функции d (x) = e^x - a x на [ a, b ]. Производная d (x) равна d¢ (x) = e^x – a. Следовательно, d¢ (x) = 0 при x * = ln (a)Î[ a, b ]. Но d¢¢ (x*) = e^x > 0, то есть x* есть точка, в которой достигается минимум функции d (x) на [ a, b ]. Очевидно, что максимум достигается в точках a или b (причем из определения a имеем d (a) = d (b)). Таким образом, b = (d (a) + d (ln(a)))/2 и d = (d (a) – d (ln(a)))/2.

Как и в случае квадратного корня, мы сможем лишь получить верхние и нижние границы для величин a, b и d (здесь можно воспользоваться механизмом интервальной арифметики). После этого остается только немного перестроить формулы, по которым вычисляются z _i, чтобы получить ¦^a.