Интервального разложения в ряд Тейлора

Любую n +1 раз непрерывно дифференцируемую функцию ¦ в окрестности точки x ^* можно разложить в ряд Тейлора

¦(x) = 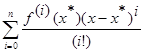+ R_n(x, x),

где

R_n(x, x) = ,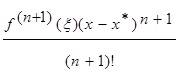

и x лежит на отрезке, соединяющим точки x и x ^*. Отсюда следует, что для любого x из интервала X значение ¦(x) будет принадлежать интервалу

T_n(X) = + ,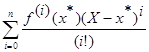

где вещественные операции заменены на соответствующие им интервальные операции и x ^*Î X. T_n(X) называется интервальным многочленом Тейлора n -го порядка. Как и для других методов, для T_n(X) справедливо условие

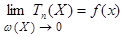
Более того, если функция ¦ бесконечное число раз непрерывно дифференцируема, то интервальное разложение в ряд Тейлора имеет то свойство, что

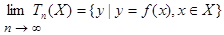
Если воспользоваться методами автоматического дифференцирования и перенести все вышеизложенное на многомерный случай, то можно значительно повысить точность оценок значений функций на параллелепипедах со сторонами, параллельными осям координат.

Схемы разбиения

Существует три схемы разбиения области: коническая, параллелепипедная и симплексная. Коническая схема, в основном, используется методами вогнутой минимизации, параллелепипедная используется методами, которые основаны на интервальной или аффинной арифметике, и симплексная схема применяется только для вогнутой минимизации.

Способы определения того, как разбивать данный параллелепипед сильно варьируются. Параллелепипед можно делить пополам вдоль самого длинного ребра, делить пополам вдоль наиболее перспективного направления, или разбивать в соответствии с длиной градиента. Можно также разбивать на k частей, где k некоторое положительное число большее, либо равное 2. Выбор конкретного разбиения определяется из условия задачи, причем для теоретической сходимости алгоритма нужно гарантировать то, что длина при таком разбиении самого длинного ребра стремится к 0.