Эффективное распределение памяти

При тестировании метода ветвей и границ на некоторых задачах обнаружилась интересная особенность. На первых этапах выполнения алгоритма скорость вычислений, произведенных с аффинными формами и с интервалами, в среднем равнялась нескольких тысячам в секунду. После того, как количество параллелепипедов в допустимом множестве достигало определенного количества, скорость вычислений неожиданно падала до нескольких сотен или даже десятков операций в секунду, даже при наличии свободной оперативной памяти. Этот эффект можно объяснить только тем, что алгоритму очень большое число раз приходится хаотично распределять и освобождать память под объекты небольшого размера, такие как параллелепипеды или вектора из аффинных форм. В результате оперативная память оказывается сильно сегментированной, и стандартный распределитель памяти становится недопустимо медлителен. Для решения этой проблемы был разработан собственный распределить памяти, базирующийся на стандартном. Общий принцип работы этого распределителя следующий. Память для объектов фиксированного размера size распределяется заранее и представляется в виде списка сегментов некоторого, достаточно большого размера, которые в свою очередь разбиты на блоки размера size, представленные в виде двух списков – свободного и занятого. Теперь, если программа затребовала кусок памяти размером size, то распределитель просто переносит блок из свободного списка в занятый и возвращает на него указатель. Это происходит, конечно, только в том случае, если свободный список не пуст, иначе распределятся новый сегмент размером, равным сумме размеров уже распределенных сегментов (т.е. итоговый размер удваивается), разбивается на блоки размера size которые, в свою очередь, добавляются в свободный список, после чего процедура повторяется. Механизм освобождения памяти происходит аналогично, нужно только определить момент, когда список сегментов не будет содержать занятых блоков и тогда освободить весь этот список.

На практике данный буферизированный распределитель оказался очень эффективным и легко применимым. Например, в одной из задач результат выполнения алгоритма содержал около полумиллиона параллелепипедов и функция разбиения этого множества на односвязные подмножества с помощью BSP-дерева (см. ниже), основанная на стандартном распределителе памяти затрачивала около 20 минут. При использовании же буферизированного распределителя потребовалось всего 6 секунд.

Структурирование результатов

На этапе завершения метода ветвей и границ результирующий список параллелепипедов может очень большим, поэтому получение такой информации как количество и содержимое связных областей, расстояние между этими областями, плотность распределения параллелепипедов в пространстве, границы результата и т.д. будет сопряжено со значительными трудностями. Поэтому нужен некоторый способ структурирования результирующего списка. В случае выбора двоичной схемы разбиения список удобно представлять в виде BSP-дерева, а в случае разбиения на k частей, в виде k -дерева. Такое дерево содержит узлы с информацией о параметрах разбиения и листья, являющиеся параллелепипедами из списка, и строится по мере выполнения алгоритма. Здесь возникает проблема построения сложных структур данных, когда один объект может одновременно принадлежать нескольким структурам данных (как, например, параллелепипеды принадлежат одновременно списку и дереву). Эта проблема может быть легко и элегантно решена путем применения механизма шаблонов языка C++.

После структурирования списка, операции по поиску какой-либо специфической информации о результате могут быть проведены быстро и эффективно.

Все описанные выше методы, а именно автоматический анализ функций, буферизированное распределение памяти и структурирование результатов были разработаны автором в виде библиотек на языке C++ и успешно протестированы на широком классе задач.

Численные результаты

Для сравнения возможностей интервальной и аффинной арифметики было проведено множество тестовых оценок примерных функций (некоторые из них показаны на графиках в приложении). Эти тесты показали, что способность аффинной арифметики учитывать взаимосвязи операндов обеспечивает в большинстве случаев значительно более точные оценки, чем в интервальной арифметике.

Ниже сравнивается выполнение IA, AA и AAIA при решении некоторых хорошо известных задач глобальной оптимизации тремя видами интервальных BAB методов: чистые модели, ускорение с локальным поиском; с ускорениями первого порядка (интервальная градиентная проверка); а также с Back-Boxing ’ом. Данные для таблиц, а также рисунки разбиения областей взяты из [7].

Поиски останавливались, когда в главном списке L не оставалось прямоугольников большего диаметра, чем определенная точность. При решении задач использовалась возрастающая точность (10^-3, 10^-6 и 10^-9) для определения влияния точности на выполнение. В таблицах ниже приведено CPU время в секундах, необходимое для решения каждой задачи каждым из вариантов, а также число прямоугольников, остающихся в L после завершения. Время ¥ означает, что программа не была завершена в течении 15 минут CPU времени.

Также даются рисунки разложений области при использовании градиентного теста и точности 0.0625% от диаметра области. На них прямоугольники, показанные белыми, были отброшены, а серые прямоугольники остались после завершения.

Задачи были запущены на машине 166Hz Pentium под Linux, используя компилятор GNU g++.

1. Функция Буфа (таблица 1, рис.3)

¦(x, y) = (x + 2 y - 7)² + (2 x + y - 5)²

Глобальный минимум ¦ в квадрате W = [-10, 10]´[-10,10] равен ¦* = 0 = ¦(1, 3). Таблица 1 содержит результаты решения этой задачи всеми вариантами.

Эта задача была выбрана потому, что она выделяет главную слабость AA: как обсуждалось ранее, AA может выполняться плохо на функциях, которые являются суммами квадратов или когда зависимость между операндами незначительна. Это привело к большему времени для AA, но только на множитель k 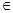[2,3].

2. Функция Exp2 (таблица 2, рис. 4)

¦(x,y) = e^xy (4 x ² + 2 y ² + 4 xy + 2 y + 1).

Глобальный минимум ¦ в квадрате W = [-10, 10]´[-10,10] есть ¦* = 0 = ¦(0.5, -1). Квадратичная часть этой функции содержит зависимости, которые позволяют AA делать намного лучшие оценки. IA- оценки возле глобального минимума оказались мало точны, что явилось следствием очень большого числа прямоугольников в списке для чистых BAB методов. С другой стороны, AA- оценки для экспоненциальной части были хуже, чем IA- оценки; как следствие метод не смог отбросить много прямоугольников, удаленных от глобального минимума.

 

Таблица 1. Результаты выполнения алгоритмов для функции Буфа

BAB -метод		Чистый		С град. проверкой		С Back-Boxing ’ом
Точность	Ариф-метика	Время	колич.	Время	колич.	время	колич.
10-3	IA AA AAIA	0.07 0.18 0.12	4 10 4	0.07 0.16 0.11	4 5 4	0.00 0.01 0.02	1 1 1
10-6	IA AA AAIA	0.12 0.34 0.19	4 10 4	0.12 0.27 0.21	4 5 4	0.00 0.01 0.00	1 1 1
10-9	IA AA AAIA	0.21 0.52 0.29	4 10 4	0.20 0.43 0.32	4 5 4	0.00 0.00 0.00	1 1 1

Рис.3. Разбиение области при минимизации функции Буфа в IA (слева), AA (в центре) и AAIA (справа).

 

Таблица 2. Результаты выполнения алгоритмов для функции Exp2

BAB -метод		Чистый		С град. проверкой		С Back-Boxing ’ом
Точность	Ариф-метика	Время	колич.	Время	колич.	время	колич.
10-3	IA AA AAIA	496.07 23.50 0.41	20610 14 14	0.29 39.34 0.48	28 5 5	0.30 38.69 0.59	30 4 5
10-6	IA AA AAIA	¥ 23.43 0.69	36727 14 14	0.44 39.44 0.75	28 5 5	0.46 38.91 0.83	28 4 5
10-9	IA AA AAIA	¥ 36.61 12.25	36635 4922 4157	0.59 40.51 1.12	32 8 8	0.61 39.51 1.18	28 7 7

 

 

Рис.4. Разбиение области при минимизации функции Exp2 в IA (слева), AA (в центре) и AAIA (справа).

Заключение

Интервальные методы ветвей и границ относительно просты для реализации и позволяют получить достаточно точные и надежные решения для широкого класса задач глобальной оптимизации. Кроме того, достаточно легко вместо интервальной арифметики использовать аффинную арифметику. Хотя аффинная арифметика действительно более точна, чем интервальная, она более сложна для реализации и более трудоемка для выполнения. Тем не менее, как показано многочисленными примерами, ее повышенная точность имеет дополнительные преимущества из-за более эффективного разбиения области, вследствие чего окончательный список параллелепипедов короче, и часто весь алгоритм работает быстрее.

Проведенные в работе исследования дают возможность решать большинство проблем, появляющихся при разработке алгоритмов решения задач глобальной оптимизации и строить оценки функций в различных арифметиках. Опыт практической реализации таких алгоритмов показывает, что большинству этих алгоритмов присущи общие характерные свойства, позволяющие реализовать их в единой системе, основанной на объектно-ориентированном подходе. Эта задача успешно решена автором данной работы. 

Очевидным следующим шагом является более полное рассмотрение задач глобальной оптимизации с ограничениями и здесь можно ожидать, что варианты, базирующиеся на аффинной арифметике, будут более эффективны.

Литература

1. Iwaarden R. Van, An Improved Unconstrained Global Optimization Algorithm, PhD the­sis, Department of Mathematics, University of Colorado at Denver, 1996. URL http://ww.cs.hope.edu/~rvaniwaa/phd.ps.gz.

2. Moore R. E., Interval analysis. New York, Prentice-Hall, 1966.

3. Glassner A., Space subdivision for fast ray tracing. // IEEE Computer Graphics & Application, 1994.

4. IEEE Standard for Binary Floating-Point Arithmetic. ANSI/IEEE Std 754-1985, IEEE, New York, 1985.

5. Comba J.L.D., Stolfi J., Affine arithmetic and its applications to computer graphics, in Proceedings of VI SIBGRAPI (Brazilian Symposium on Computer Graphics and Image Processing), 1993, pp. 9-18. URL http://dcc.unicamp.br/~stolfi/.

6. Figueiredo L.H. DE, Surface intersection using affine arithmetic, in Pro­ceedings of Graphics Interface '96, May 1996, pp. 168-175. URL ftp://csg.uwaterloo.ca/pub/lhf/gi96.ps.gz.

7. Figueiredo L.H. DE, Stolfi J., Adaptive enumeration of implicit surfaces with affine arithmetic, Computer Graphics Forum, 15 (1996), pp. 287-296.

8. Figueiredo L.H. DE, Stolfi J., Iwaarden R. Van, Branch-and-bounds methods for unconstrained global optimization with affine arithmetic.

9. Farouki R., Rajan V., Algorithms for polynomials in Bernstein form, Computer Aided Geometric Design, 5 (1988), pp. 1-26.

10. Gill P.E., Murray W., Wright H., Practical Optimization, Academic Press, San Diego, CA, 1981.

11. Hansen E., A generalized interval arithmetic, in Interval Mathematics, K. Nickel, ed., no. 29 in Lecture Notes in Computer Science, Springer Verlag, 1975, pp. 7-8

12. Назаренко Т.И., Марченко Л.В., Введение в интервальные методы вычислительной математики, 1982

13. Калмыков С.А., Шокин Ю.И., Юлдашев З.Х., Методы интервального анализа, 1986

14. Шокин Ю.И., Интервальный анализ, 1981

15. Кнут Д., Искусство программирования для ЭВМ, Т.1, 1976

16. Коллатц Л., Крабс В., Теория приближений. Чебышевские приближения и их приложения, Москва “Наука” 1978

 

Приложение
Примеры оценивания диапазонов функций

На ниже приведенных рисунках оценки функций выражены множеством прямоугольников. Вертикальные стороны каждого прямоугольника обозначают отрезок изменения аргумента, горизонтальные обозначают оцененный диапазон функции на данном отрезке.

 

Рис. 1. , ¦(¦(x)) оценивается на отрезке [-1,1] c шагом 0.0125 в интервальной арифметике.

 

Рис. 2. , ¦(¦(x)) оценивается на отрезке [-1,1] c шагом 0.0125 в аффинной арифметике.

 

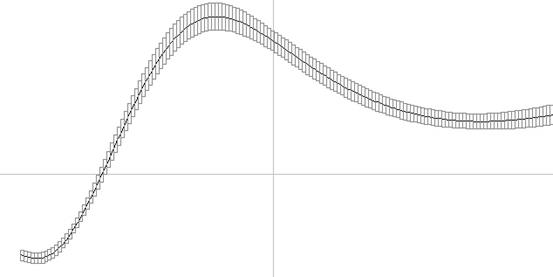
Рис. 3. , ¦(¦(x)) оценивается на отрезке [-1,1.2] c шагом 0.0126 в интервальной арифметике.

 

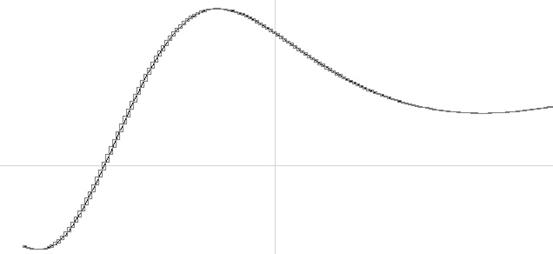
Рис. 4. 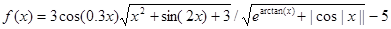, ¦(¦(x)) оценивается на отрезке [-1,1.2] c шагом 0.0126 в аффинной арифметике.