3.1. Следующим этапом работы по созданию алгоритмов расчета сеток является переход от дифференциальной формы вариационного функционала к дискретной. Мнение о том, что этот этап сводится к механической замене дифференциальных выражений разностными, является ошибочным. При такой замене могут быть утеряны важные свойства дифференциальной модели. Рассматриваемая задача может служить иллюстрацией такой ситуации.
Для того, чтобы правильно передать обращение в нуль якобиана отображения при разностной аппроксимации функционала (1.1), может быть использована специальная процедура, известная под названием вариационного барьерного метода. Она была разработана для расчета гармонических сеток, хорошо известна и многократно описана. Поэтому не будем на ней останавливаться. Изложим окончательный результат, представленный в работе [2], имеющий непосредственное отношение к функционалу (1.1), с некоторыми (более привычными для нас) изменениями (в основном – в обозначениях).
Рассматривается задача построения двумерной регулярной сетки
(3.1) 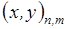 ,
, 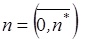 ,
, 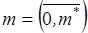
при заданных координатах граничных узлов
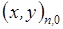 ,
, 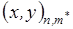 ,
,  ,
, 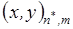
на контуре, ограничивающем односвязную область W на плоскости (х,у).
Пусть координаты (х,у) n,m узлов сетки заданы (можно говорить о них, как о некотором исходном приближении для искомой сетки). Рассмотрим ячейку сетки и занумеруем вершины, обходя ее контур против часовой стрелки: узлу (n,m) присвоим номер k =1, узлу (n +1, m) - номер k =2, узлу (n +1, m +1) - k =3, узлу (n,m +1) - номер k =4. В последующих выражениях следует полагать k -1=4 при k =1 и k +1=1 при k =4.
Ячейке с такими вершинами обычно присваивают громоздкий «полуцелый» номер (n +1/2, m +1/2). Вместо этого условимся о присвоении ей менее громоздкого номера 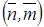 , отмечая верхней чертой условное прибавление +1/2. Соответственно
, отмечая верхней чертой условное прибавление +1/2. Соответственно  заменит номер
заменит номер
(n -1/2, m -1/2), 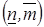 - номер (n -1/2, m +1/2), наконец
- номер (n -1/2, m +1/2), наконец 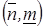 - номер (n +1/2, m -1/2).
- номер (n +1/2, m -1/2).
Дискретный аналог функционала (1.1) записывается тогда в виде:
(3.2) 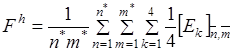
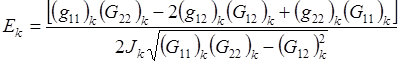 ,
,
где
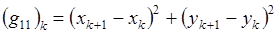
(3.3) 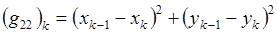
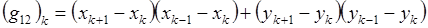
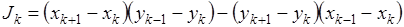
Будем предполагать, что все Jk >0 для всех ячеек сетки, т.е. все ячейки сетки – выпуклые четырехугольники. Такую сетку будем называть выпуклой (автор [2] называет ее невырожденной).
(G11, G12, G22) k - элементы симметричных положительно определенных матриц Gk, отнесенных к треугольнику с номером k в ячейке с номером 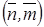 .
.
Непосредственной проверкой можно убедиться в тождественном выполнении соотношения
(3.4) 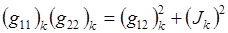 ,
,
которое является разностным аналогом тождества (1.6). Если, в соответствии с (1.5), назначить элементы матриц Gk формулами:
(3.5) 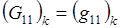 ,
, 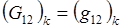 ,
, 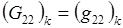 ,
,
то оказывается, что 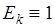 для всех k и всех ячеек сетки
для всех k и всех ячеек сетки  ,
, 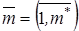 .
.
Следовательно, для заданной сетки (3.1) получаем по формулам (3.2) значение Fh =1, т.е. абсолютный минимум этой суммы, представляющей дискретный аналог функционала (1.1). Таким образом, задание элементов матриц G формулами (3.5) реализует заданную произвольным образом выпуклую (невырожденную) сетку (3.1) как решение задачи минимизации дискретного функционала Fh.
В работе [2] доказано, что сетка принадлежит к классу выпуклых (невырожденных) сеток тогда и только тогда, когда она минимизирует функционал (3.2) для некоторого набора положительно определенных и симметричных матриц Gk.
3.2. Аналогичный дискретный функционал можно было бы построить и для (1.10):
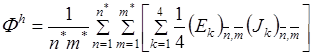
Но мы поступим иначе. Заменим в нем внутреннюю сумму для четырех треугольников одной ячейки одним слагаемым следующего вида:
(3.6) 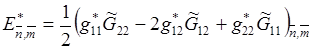
Величины в правой части (3.6) будем вычислять без разбиения ячейки на треугольники по формулам, которые для краткости используют описанную выше нумерацию вершин ячейки:
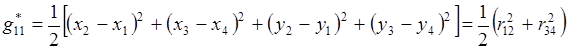 ,
,
(3.7)
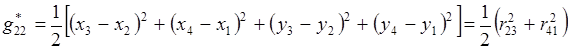 ,
,
где 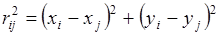 .
.
Для площади ячейки J* и площадей треугольников sk = Jk /2 имеем:
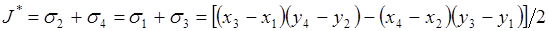 .
.
Пусть jk – угол в вершине ячейки с номером k. Тогда
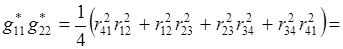
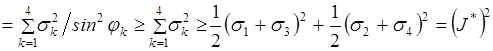 .
.
Чтобы обеспечить выполнение тождества, аналогичного (3.4), определим величину 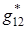 формулой:
формулой:
(3.8) 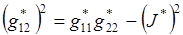
Заметим, что формула (3.8) определяет величину 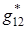 только с точностью до знака. Однако этого будет достаточно при тех вариантах назначения G12, которые рассматриваются ниже в § 4.
только с точностью до знака. Однако этого будет достаточно при тех вариантах назначения G12, которые рассматриваются ниже в § 4.
Аппроксимируем функционал (1.10)-(1.11) суммой
(3.9) 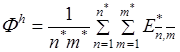
 2020-01-14
2020-01-14 215
215








