О численных алгоритмах минимизации функционалов

 

5.1. Чтобы получить непосредственное представление о степени сложности уравнений, которые придется решать при минимизации вариационных функционалов, выпишем уравнения Эйлера-Лагранжа для функционала (1.1). Как уже отмечалось в § 1, эти уравнения имеют вид (1.12). Формулу для Е запишем в виде:

(5.1) ,

где g₁₁, g₁₂, g₂₂ определены формулами (1.2).

Метрические параметры  ,  ,  будем считать функциями независимых переменных (x,h), хотя в соответствии с изложенными в

§ 4 вариантами их назначения следовало бы учитывать и более сложный характер их зависимости от производных x_x, y_x, x_h, y_h.

Здесь уместно напомнить о целесообразности замены якобиана в знаменателе на величину J_e, определенную формулой (1.19).

Необходимые для выписывания уравнений (1.12) производные 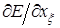, , ,  получаются непосредственным дифференцированием (5.1) и после некоторых преобразований приобретают следующий вид:

      

(5.2)

     

     

Заметим, что в частном случае гармонических отображений ,  формулы (5.2) заметно упрощались и, кроме того, удавалось в качестве следствия из получающихся для этого случая уравнений (1.12) получить очень изящные уравнения:

(5.3)                       

                                .

Принято считать, что применение уравнений (5.3) в практике расчета сеток восходит к работе [18].

5.2. Изложение численных алгоритмов минимизации вариационных функционалов представляет весьма сложную задачу. Поэтому ограничимся в качестве иллюстрации только некоторыми простейшими случаями. В качестве первого из них рассмотрим вариационный функционал (1.10)-(1.11), дискретизация которого осуществляется без разрезания ячеек сетки на треугольники посредством использования формул (3.6)-(3.9), а в качестве метрических параметров G₁₁, G₂₂ используются вычисленные посредством интерполяции в разделе 4.2. и G₁₂ =0.

Разностные уравнения, которым должны удовлетворять координаты искомой сетки (x,y)_n,m, получаются как условия равенства нулю производных соответствующей вариационному функционалу интегральной суммы:

(5.4)  , ,   ,

Такие уравнения выписываются для всех внутренних узлов искомой сетки, значения же координат граничных узлов предполагаются заданными. В интегральной сумме (3.9) от координат узла с фиксированным номером (n,m) будут зависеть только 4 слагаемых, отвечающих 4 ячейкам сетки с номерами , , , , согласно обозначениям, описанным в разделе 3.1. Эти 4 ячейки образуют так называемый шаблон узла. Для его описания удобно, как это предложено в работе [17], присвоить 9 узлам сетки следующие «простые» номера:

(5.5)               

            

            

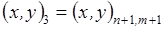
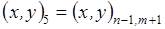
Условно доопределим .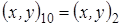

Тогда шаблон образует 4 ячейки с номерами , где ячейка с номером L имеет вершины с «простыми» номерами 1, 2 L, 2 L +1, 2 L +2.

Обозначим 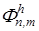 «элемент» интегральной суммы Ф^h, зависящий от искомых координат . Тогда

(5.6) ,

где в соответствии с формулой (3.6) и с учетом G₁₂ =0:

(5.7)

Величины ,  вычисляются по формулам (4.2).

Для получения уравнений (5.4) достаточно дифференцировать «элемент» (5.6). Выбранная форма (3.7) для величин  позволяет получить уравнения (5.4) для описанного выше шаблона в виде:

(5.8)       ,   .

Коэффициенты C_L вычисляются по формулам:

(5.9)                 ,

где следует полагать L- 1=4 для L =1.

Вопрос о решении системы линейных уравнений (5.8), выписанных для всех внутренних узлов сетки, может быть предметом специального обсуждения. В практических расчетах нестационарных задач используется простейший вариант: выполняется несколько явных итераций, в ходе которых новое положение ,  узла (х₁,у₁) получается по формулам:

(5.10)             ,

                      ,

где , 0<w<1 – некоторый коэффициент «запаса», задаваемый в качестве управляющего параметра. Конечно, это очень медленно сходящийся итерационный процесс. Простейшим способом его улучшения является использование вместо w переменной последовательности чебышевских параметров. Однако он практически работоспособен, а предметом обсуждения сейчас являются совсем другие вопросы.

5.3. В качестве второго случая численной минимизации рассмотрим случай, когда вариационный функционал задается в форме (1.10)-(1.11), а метрические параметры G₁₁, G₂₂, G₁₂ назначаются, как описано в разделе 4.3, изменяющимися в ходе итерационного процесса, например, согласно формулам (4.5).

Рассмотрим сначала случай, когда параметр p_*= 0 и, следовательно G₁₂ =0. Тогда для расчета сетки получаются те же формулы (5.9)-(5.10). Отличие состоит лишь в том, что при вычислении коэффициентов C_L величины G₁₁, G₂₂, как уже отмечено, назначаются по формулам (4.5) и изменяются на каждой итерации. Вместо системы линейных уравнений реализуется решение некоторой нелинейной системы. Проблему сходимости итерационного процесса и скорости, с которой это происходит, сейчас обсуждать не будем.

Обратимся к более общему случаю, когда управляющий параметр p_*¹ 0. Тогда формула (5.7) должна быть заменена на следующую:

(5.11)          

Появляющаяся в ней величина  аппроксимируется формулой (3.8). Выше при рассмотрении случая p_*=0 величины G₁₁, G₂₂ вычислялись по состоянию сетки на последней сосчитанной итерации и при получении уравнений (5.8) предполагались «замороженными». Наличие в формуле (5.11) величины  в числителе и знаменателе вынуждает выбрать один из трех путей.

а) «Заморозим» 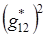 и в числителе и в знаменателе. Тогда получим те же уравнения (5.8), а формулы (5.9) должны быть заменены на

       , .

Такой путь представляется весьма сомнительным.

б) «Заморозим» 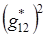 только в знаменателе. Тогда в уравнениях (5.8) появятся дополнительные члены, включающие величины x_2L+1, y_2L+1 со своими коэффициентами. Конкретизировать их вид не будем.

в) Формула (5.11) порождает нелинейный функционал. Он рассматри-вается как ситуация общего вида, к обсуждению которой и перейдем.

5.4. В работе [17] представлен алгоритм прямой минимизации вариационного функционала произвольного вида. Алгоритм носит локальный характер. Для каждого узла сетки независимо решается задача отыскания его нового положения, уменьшающего значение рассматриваемого функционала, в предположении, что все другие узлы сетки при этом остаются фиксированными («замороженными»).

  Схема метода спуска состоит в следующем. В рассматриваемом узле назначается направление спуска. Вычисляются коэффициенты локальной параболической аппроксимации функционала и находится точка с минимальным значением функционала на выбранном направлении. В качестве нового приближения назначается точка на выбранном направлении с некоторым коэффициентом «запаса».

Численные эксперименты (в частности, с функционалами для расчета сеток, рассматривавшимися в работе [11]) подтвердили работоспособность обсуждаемого алгоритма, хотя и крайне медленную его сходимость.

В условиях большой сложности уравнений, описанных выше в разделе 5.1., трудно усмотреть практическую альтернативу такому пути численной минимизации разработанных функционалов для построения сеток. Поэтому ограничимся изложенным.