Индийские математики, начиная с Брахмагупты (VII в. н. э.), систематически пользовались отрицательными числами и трактовали положительное число как имущество, а отрицательное — как долг. Брахмагупта приводит все правила арифметических действий над отрицательными числами. Ему еще не была известна двузначность квадратного корня, но уже в 850 г. Магавира в своей книге «Ганита-сара-санграха» («Краткий курс математики») пишет: «Квадрат положительного или отрицательного — числа положительные, их квадратные корни будут соответственно положительными и отрицательными. Так как отрицательное число по своей природе не является квадратом, то оно не имеет квадратного корня». Последние слова Магавиры показывают, что он ставил вопрос и об извлечении корня из отрицательного числа, но пришел к выводу, что эта операция невозможна. Не исключено, что об отрицательных числах индийские ученые узнали в результате контактов с китайской наукой. Прямых свидетельств в пользу такого предположения мы не имеем. Во всяком случае, в Индии отрицательные числа не применялись при решении систем линейных уравнений (мы не находим здесь ничего подобного методу фан-чэн). Индийцы называли положительные числа «дхана» или «сва» (имущество), а отрицательные — «рина» или «кшайа» (долг).
Индийцы применяли символ квадратного корня «му» не только к полным квадратам, но и к полученным квадратичным иррациональностям. Бхаскара с помощью правил

и

заимствованных, быть может, у греков, производил преобразования квадратичных числовых иррациональностей и таким образом упрощал довольно сложные выражения, как, например,

Возможно, что исходными здесь были преобразования правой части. Некоторые преобразования, например,

могли использоваться для более удобного приближенного извлечения корней.
Такое свободное пользование иррациональностями также было воспринято в странах ислама, где Омар Хайям в XI в. предложил расширить понятие числа до того, что мы называем положительным иррациональным числом.
Линейные уравнения
Задачи, приводящие к решению линейного уравнения с одним неизвестным, имеются у Ариабхаты. К линейному уравнению, в частности, приводит его задача, обошедшая в дальнейшем под названием «задачи о курьерах» мировую алгебраическую литературу,— она приводится и в нынешних школьных руководствах. В этой задаче требуется определить время встречи двух небесных светил но данным скоростям v1, v2 и расстоянию a» между ними. Ариабхата сообщает решение
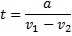
при движении в одну сторону; если v1<v2, то встреча произошла в прошлом. При движении навстречу необходимо расстояние разделить на сумму скоростей. О случае, когда встреча произошла в прошлом, Ариабхата не упоминает, и мы не знаем, рассматривает ли он этот случай или нет, так же как не знаем, были ли ему известны отрицательные числа. Впрочем, вряд ли он умел истолковать отрицательное значение t, соответствующее v1<v2. Индийские математики и позднее не принимали в расчет отрицательные решения уравнений и для этого изменяли подходящим образом условия задач.
Заметим, что «задачи о курьерах» в некоторых более сложных вариантах (например, движение с переменной скоростью, растущей в арифметической прогрессии) приводят и к квадратному уравнению,— такой пример есть уже в «Бахшалийской рукописи».
У Магавиры, Бхаскары и других авторов имеются задачи, приводящие к системам линейных уравнений с несколькими неизвестными. Так, одна из задач Магавиры приводит к системе

Метод решения, изложенный Магавирой, не отличается от современного метода решения при помощи уравнивания коэффициентов.
Однако дело не ограничивалось столь простыми задачами. Были выработаны правила решения систем вида

(складывая все уравнения почленно, находили  ) других, несколько более общих, например:
) других, несколько более общих, например:

Разумеется, речь шла всегда о задачах с численными условиями, но правила формулировались в общем виде. Такие задачи встречаются, постепенно усложняясь, у Ариабхаты, Брахмагупты, Магавиры, Нарайаны. Но, как мы уже сказали, общего алгоритма вроде метода фан-чэн индийские математики не создали.
Квадратные уравнения
Задачи на квадратные уравнения имеются в «Ведах» и «Шулва-сутре», но с решением их мы впервые встречаемся, по-видимому, у Ариабхаты. Так, задача на сложные проценты приводит к уравнению

Решение этого уравнения, приведенное Ариабхатой словесно, можно записать в виде

Подобного рода задачи, так же как «задачи о курьерах», приводились затем многими авторами как в Индии, так и в других странах. С такой задачи начинал раздел квадратных уравнений в своем широко известном учебнике алгебры А. Клеро (1746). К квадратному уравнению приводит также задача на определение числа членов арифметической прогрессии по данным сумме, первому члену и разности.
Немного спустя квадратные уравнения появляются в «Бахшалийской рукописи». Примерно в это же время большой вклад в решение квадратных уравнений внес Брахмагупта, который сформулировал общее правило решения квадратных уравнений, приведенных к канонической форме

где коэффициент при неизвестной первой степени b и свободный член с могут принимать и отрицательные значения.
Решение Брахмагупты такое же, как у Ариабхаты. Шридхара словесно формулирует решение в несколько другом виде:

Брахмагупта еще не говорит о двух корнях квадратного уравнения, но Магавира уже знает об этом, что видно из его задачи, в которой требуется найти число павлинов в стае, 1/16 которой, умноженная на себя, сидит на манговом дереве, а квадрат остатка вместе с 14 другими павлинами — на дереве тамала. Магавира приводит эту задачу к уравнению

и формулирует решение квадратного уравнения вида
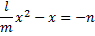
с помощью правила

говоря, что «квадратный корень можно как прибавлять, так и вычитать». В нашем случае условиям задачи удовлетворяет только корень 48, так как корень  дробный.
дробный.
Бха скара уже формулирует условие существования двух положительных корней.
Индийцы решали и системы уравнений; например, Бхаскара решал задачу об определении катетов xиy и гипотенузы z прямоугольного треугольника по его периметру и площади, сводящуюся к системе

Бхаскара рассматривал также специально подобранные уравнения третьей и четвертой степеней, целочисленные корни которых он находил путем несложных преобразований. Так, уравнение

Бхаскара решает следующим образом: прибавляя к обеим частям  , он получает
, он получает
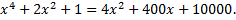
Извлечение корня из обеих частей дает

откуда

Площади и объемы
Сведения по геометрии имеются также в трактатах Брахмагупты, Магавиры, Шридхары, Бхаскары.
Брахмагупта приводит приближенное правило для вычисления площади произвольного четырехугольника как произведения полусумм противоположных сторон, с которым мы встречались в математике египтян и вавилонян.
Шридхара указывал, что это правило нельзя применять ко всем четырехугольникам. Он сообщает точное правило вычисления площади трапеции.
Брахмагупта для нахождения площади четырехугольника пользовался правилом, аналогичным правилу Архимеда — Герона для площади треугольника:
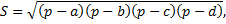
где а, b, с и d — стороны четырехугольника, а p — полупериметр. Это правило верно только для четырехугольников, вписанных в круг. Брахмагупта не оговаривает этого, но фактически рассматривает лишь два типа четырехугольников — равнобедренные трапеции и четырехугольники с пересекающимися под прямым углом диагоналями, для которых правило справедливо.
Геометрические доказательства крайне лаконичны, но нередко весьма наглядны. Так, для обоснования правила вычисления площади треугольника приводится рисунок, в котором высота прямоугольника равна половине высоты треугольника (рис. 4). Для обоснования предложения «Площадь круга равна площади прямоугольника,


рис.4 рис.5
стороны которого соответственно равны полуокружности и радиусу». Ганеша (XVI в.) делит круг на 12 равных секторов, а затем разворачивает каждый полукруг, состоящий из 6 секторов, в пилообразную фигуру, основание которой равно полуокружности, а высота — радиусу (рис. 5). Прямоугольник, о котором говорится в условии, получится при вставлении зубьев одной из «пил» в зазоры между зубьями другой. По-видимому, читатель должен был представить себе, что круг разделен не на 12, а на столь большое число секторов, что эти секторы станут неотличимы от треугольников, составляющих «пилы».
Приближенные выражения отношения длины окружности к диаметру мы находим уже в сиддхантах. В «Пулисе-сиддханте» (V в. н. э.) говорится, что длина окружности относится к диаметру, как 3927 к 1250, что соответствует значению π = 3,1416. То же значение π в виде 
мы находим у Ариабхаты. Брахмагупта пользовался приближением  , возможно, китайского происхождения. Встречается у индийцев и приближение π = 22/7. В сиддхантах, как и у александрийских астрономов, окружность делится на 360 градусов, каждый градус — на 60 минут, но радиус делится не на 60 частей, а на 3438 минут. Это объясняется тем, что, если считать окружность равной 360
, возможно, китайского происхождения. Встречается у индийцев и приближение π = 22/7. В сиддхантах, как и у александрийских астрономов, окружность делится на 360 градусов, каждый градус — на 60 минут, но радиус делится не на 60 частей, а на 3438 минут. Это объясняется тем, что, если считать окружность равной 360  60 = 21 600 минутам, а π = 3,1416, то из соотношения С = 2πr, мы найдем, что r = 3437,7 минут. Как мы видим, индийцы измеряли радиус в долях окружности уже в V в., поэтому возможно, что приведенная выше «теорема Ганеши» была известна индийцам задолго до Ганеши. Возможно также, что в чертеже Ганеши предполагалось, что круг разделен на 3438 секторов.
60 = 21 600 минутам, а π = 3,1416, то из соотношения С = 2πr, мы найдем, что r = 3437,7 минут. Как мы видим, индийцы измеряли радиус в долях окружности уже в V в., поэтому возможно, что приведенная выше «теорема Ганеши» была известна индийцам задолго до Ганеши. Возможно также, что в чертеже Ганеши предполагалось, что круг разделен на 3438 секторов.
Шридхара приводит правила вычисления объема призмы V = SH, объема усеченного кругового конуса
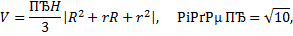
и объема кругового конуса  .
.
Бхаскара дает правило вычисления объема шара
 где π = 3,1416.
где π = 3,1416.
 2020-01-14
2020-01-14 288
288








