Уравнения в вариациях

Рассмотрим задачу Коши:

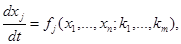(14)

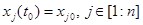(15)

 

где 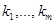 - параметры. В дальнейшем мы рассмотрим функционалы, зависящие от параметров  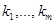через решение задачи Коши (14),(15). Тогда градиентные уравнения будут зависеть от производных по  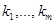решения задачи (14),(15), и мы должны уметь их вычислять. Дифференцируя уравнения (14), (15) по  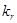получаем, что функции

 

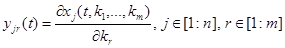 (16)

 

удовлетворяют следующей задаче Коши:

 

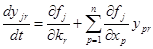   (17)

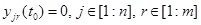  (18)

 

Уравнения (17) относительно производных (16) называют уравнениями в вариациях для уравнений (14).

 

Функционалы метода наименьших квадратов

Мы не можем рассмотреть здесь все многообразие функционалов метода наименьших квадратов и ограничимся одним достаточно общим функционалом. Он соответствует следующей задаче: модель некоторого процесса описывается задачей Коши (14),(15) (такие модели, в частности, достаточно распространены в биологической кинетике), даны измерения

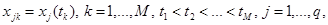, (19)

 

то есть даны 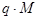 приближений для значений величин  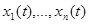в моменты времени 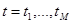, и требуется найти параметры  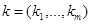на основе заданного начального приближения .

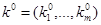В методе наименьших квадратов нахождения (идентификации) параметров  рассматривают функционал

 

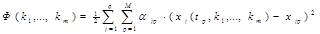  (20)

 

где 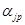 - фиксированные весовые коэффициенты, а  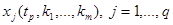- значения первых  компонент решения задачи (14),(15) в точке 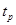 при заданных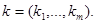

В методе наименьших квадратов полагают, что значение 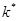, доставляющее минимум этой функции 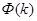, является адекватным приближением к реальному значению параметра  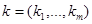для принятой модели процесса.

Для того, чтобы воспользоваться методом градиентных уравнений, необходимо выписать уравнения (7) для функционала (20):

 

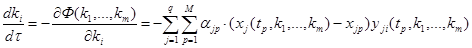 (21)

 

Эти градиентные уравнения надо дополнить начальными условиями:

 

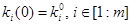(22)