Численное решение градиентных уравнений

Обратимся к функционалу 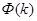, , 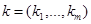определенному в п.1.3. Пря-мой способ нахождения приближенного значения точки 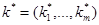, определенной по формуле (17) (то есть точки предполагаемого минимума функционала ), – это численное интегрирование градиентных уравнений (21) при начальных условиях (22).

Правые части уравнений (21) зависят от неизвестных  через значения функций 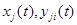 в точках  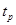при 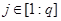, , 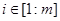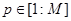. При фиксированных значениях  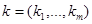величины  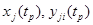могут быть получены численным интегрированием уравнений (14),(17) при начальных условиях (15),(18).

Таким образом, нам надо обсудить численные методы интегрирования за-дачи Коши для обыкновенных дифференциальных уравнений. Наиболее рас-пространены пошаговые методы, которые позволяют для задачи Коши

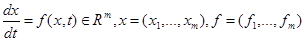, (23)

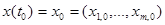,                 (24)

отправляясь от значения 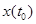, последовательно получать приближенные значения  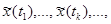решения в точках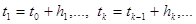

Числа 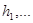 называют шагами интегрирования, а числа 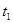,…- узлами таблицы или сетки численного интегрирования. Совокупность узлов называют сет-кой, а величины  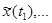называют значениями решения на узлах сетки. Если  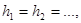то говорят о равномерной сетке или об интегрировании с постоянным шагом.

Численное интегрирование градиентных уравнений, как правило, требует частой смены величины шага интегрирования. Хорошо к быстрой смене шага приспособлены явные методы Рунге-Кутта и метод рядов Тейлора.

Пошаговые методы численного интегрирования обыкновенных дифференциальных уравнений хорошо освещены в литературе по численному анализу (см., например, [2,3]).