2020-01-14
154
Для составления эконометрической модели национальной экономики Турции идентифицируем следующую эконометрическую модель:
,
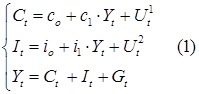, где
,
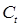- потребление за год 
,
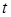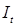- инвестиции за год ,
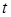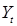- ВВП за год 
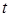(без чистого экспорта и прироста запасов),
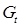- государственные расходы за год 
,
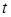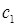- склонность к потреблению,
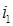- склонность к инвестированию,
, 
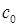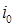- свободные члены уравнения,
, 
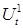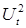- случайные остатки уравнения.
В этой системе три эндогенных переменных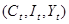 
и одна экзогенная переменная 
.
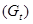Проверим модель на идентифицируемость:
Необходимое условие:
1-е уравнение:
H=2 (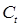, 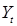) D=1()
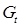D+1=H => уравнение точно идентифицируемо
2-е уравнение:
H=2 (,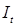 
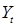) D=1(
)
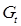D+1=H => уравнение точно идентифицируемо
Достаточное условие:
1-е уравнение:
|
|
| |
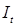
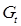
| 2 | -1 | 0 |
| 3 | 1 | 1 |
det = -1 ≠ 0
rang = 2
Число эндогенных переменных равно 3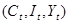 
, 3-1=2, т.е. ранг равен числу эндогенных переменных без одного => уравнение точно идентифицируемо.
2-е уравнение:
|
|
| |
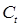
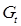
| 1 | -1 | 0 |
| 3 | 1 | 1 |
det = -1 ≠ 0
rang = 2
Число эндогенных переменных равно 3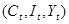 
, 3-1=2, т.е. ранг равен числу эндогенных переменных без одного => уравнение точно идентифицируемо.
Из необходимого и достаточного условий следует, что система точноидентифицируема, применяется КМНК (косвенный метод наименьших квадратов).
Идентификация модели состоит в нахождении по исходным данным оценок коэффициентов модели c0, с1, i0, i1 для структурной формы модели.
Приведем систему уравнение модели к структурному виду, в которой нет балансовых переменных. Подставим для этого балансовую переменную в остальные уравнения.
Исключим из системы уравнений (1) балансовое уравнение:
, ,
. .
,
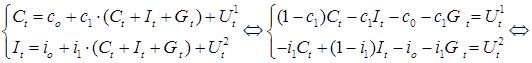
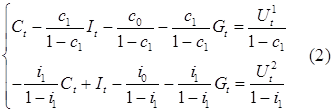
- структурная форма модели
.
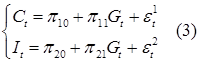Разрешаем уравнение структурной формы (2) относительно эндогенных переменных 
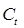и 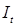и получаем приведенную форму модели:
,
. где
,
,
,
,
,
.
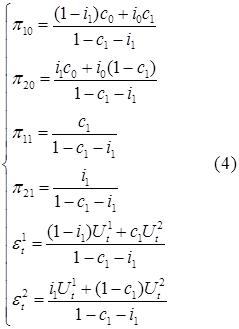
Проведя вычисления с помощью программы Excel, используя МНК (см. таблицы № 2,3 Приложения), получим следующие оценочные коэффициенты. Чтобы упростить процедуру расчетов будем работать с отклонениями от средних уровней, т.е. Сt - Сt, Gt - Gt, It - It.
Система нормальных уравнений в общем виде:
∑y = na + b1∑x1 + b2∑x2 + … +bp∑xp,
∑yx1 = a∑ x1 + b1 ∑ (x1)2 + b2∑x1x2 + … + bp∑xpx1, (5)
…………………………………………………….,
∑yxp = a∑xp + b1 ∑x1xp + b2 ∑x2xp + … + bp∑(xp)2.
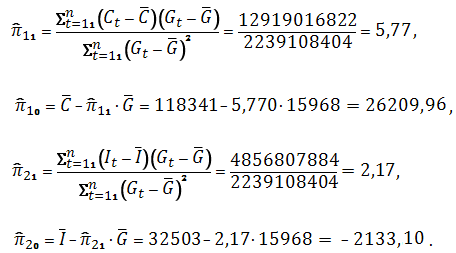Из системы нормальных уравнений для каждого из уравнений следует, что:
(6)
Подставив найденные оценки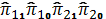 
в систему (3), получим:
Ĉ = 26209,95+5,77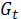 
,
Î = -2133,10+ 2,17 .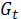
Теперь найдем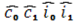 
на основании системы (4):
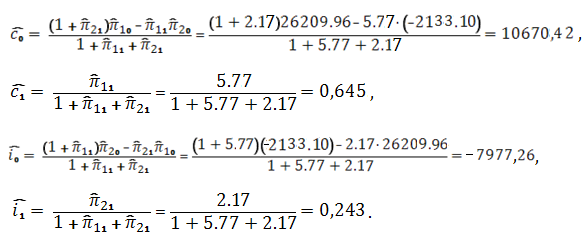
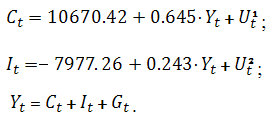
Подставим полученные коэффициенты в исходную модель (1):
2
