Теперь мы готовы для квази-средних указать упомянутое выше аксиоматическое определение. Будем исходить от частных случаев – простейших средних. Так взвешенные среднее арифметическое  и среднее геометрическое
и среднее геометрическое 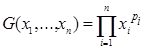 можно определить как непрерывные хотя бы в одной точке решения функциональных уравнений
можно определить как непрерывные хотя бы в одной точке решения функциональных уравнений 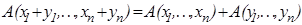 и
и 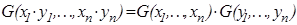 соответственно, а также эти решения должны удовлетворять условию усреднения, иначе не обязательно
соответственно, а также эти решения должны удовлетворять условию усреднения, иначе не обязательно 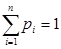 и
и  . Первое условие есть результат теоремы 1, а второе условие мы докажем далее в общем случае.
. Первое условие есть результат теоремы 1, а второе условие мы докажем далее в общем случае.
Заметим, что операцию умножения, которая используется в уравнении для среднего геометрического, можно представить как 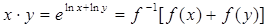 , где
, где  , то есть функция, задающая среднее геометрическое. Операция сложения в уравнении для среднего арифметического представляется аналогично, но с функцией
, то есть функция, задающая среднее геометрическое. Операция сложения в уравнении для среднего арифметического представляется аналогично, но с функцией 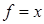 .
.
Тогда вообще для квази-средних рассмотрим операцию, обобщающую сложение и умножение, 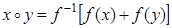 , где
, где 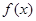 – произвольная непрерывная, строго монотонная функция, множество значений которой – один из промежутков (–
– произвольная непрерывная, строго монотонная функция, множество значений которой – один из промежутков (–  ;а), (–
;а), (–  ;а], (b;
;а], (b; 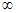 ), [b;
), [b; 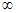 ), (–
), (– 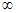 ;
; 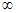 ), где a≤0 и b≥0, что гарантирует существование операции для любых x и y из области определения функции
), где a≤0 и b≥0, что гарантирует существование операции для любых x и y из области определения функции 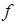 . Сформулируем общий результат, выражающий аксиоматическое определение квази-средних [1].
. Сформулируем общий результат, выражающий аксиоматическое определение квази-средних [1].
Теорема 2. Квази-средние – это такие функции 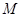 от n переменных, для которых выполнены условия:
от n переменных, для которых выполнены условия:
1) непрерывность хотя бы в одной точке;
2) 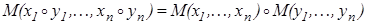 ;
;
3) 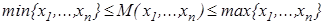 .
.
Доказательство. Очевидно, что квази-средние, ранее определённые как  удовлетворяют перечисленным свойствам. Важно показать обратное – других величин с данными свойствами не существует. Для этого выведем вид функций
удовлетворяют перечисленным свойствам. Важно показать обратное – других величин с данными свойствами не существует. Для этого выведем вид функций 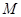 , исходя из указанных условий.
, исходя из указанных условий.
Распишем уравнение  , используя определение операции
, используя определение операции 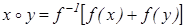 :
:
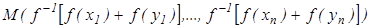 =
=
= 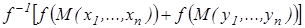 ,
,
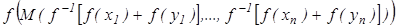 =
=
= 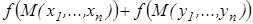
Далее, если определить 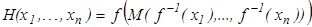 иобозначить
иобозначить 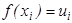 ,
, 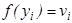 , то последнее выражение перепишется так
, то последнее выражение перепишется так 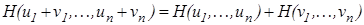 , где функция H непрерывна хотя бы в одной точке. Тогда единственной такой функцией будет
, где функция H непрерывна хотя бы в одной точке. Тогда единственной такой функцией будет 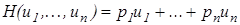 , pi
, pi 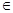 R. Возвращаясь к прежним переменным и функциям, найдём
R. Возвращаясь к прежним переменным и функциям, найдём 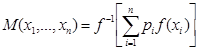 , pi
, pi  R.
R.
Осталось показать, что  и
и  . Используем свойство усреднения найденного решения:
. Используем свойство усреднения найденного решения: 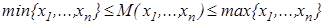 .
.
Возьмём 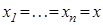 , но тогда
, но тогда 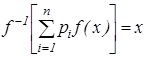 или
или  , и поэтому
, и поэтому 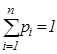 . А если предположить, что какое-то
. А если предположить, что какое-то 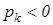 , то для
, то для 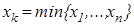 и
и  ,
, 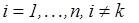 имеем
имеем
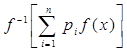 =
= 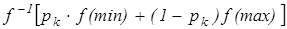 =
=
= 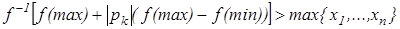 , что противоречит условию.
, что противоречит условию.
Аналогично можно определить квази-средние вида 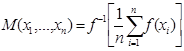 .
.
Теорема 3. Квази-средние вида 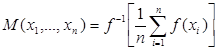 – это такие функции
– это такие функции 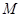 от n переменных, для которых выполнены условия:
от n переменных, для которых выполнены условия:
1) непрерывность хотя бы в одной точке;
2)  ;
;
3) рефлексивность, то есть 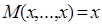 ;
;
4) симметричность.
Действительно, свойства 1 и 2 выделяют функции 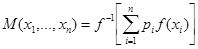 , pi
, pi 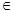 R, далеесвойство 3 обеспечивает
R, далеесвойство 3 обеспечивает 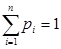 , а из свойства 4 вытекает
, а из свойства 4 вытекает 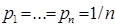 .
.
Теперь мы можем аксиоматически задавать частные случаи квази-средних, указывая для них свои операции в функциональном уравнении 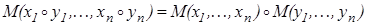 . Например:
. Например:
для среднего арифметического 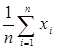 задающая его функция
задающая его функция 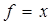 , и поэтому
, и поэтому 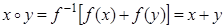 ;
;
для среднего геометрического 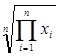
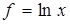 ,
, 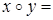
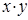 ;
;
для среднего гармонического 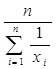
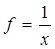 ,
, 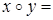
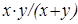 ;
;
для среднего квадратичного 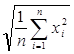
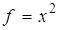 ,
, 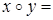
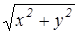 .
.
 2020-01-14
2020-01-14 112
112