Теорема 1. Единственными непрерывными хотя бы в одной точке решениями следующих уравнений являются соответственно функции:
1. 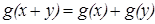
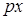 ;
;
2. 
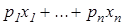 ;
;
3. 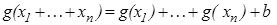
 ;
;
4. 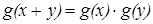
 ;
;
5. 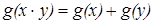
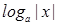 ;
;
6. 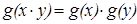
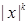 и
и 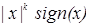 , x≠0;
, x≠0;
7. 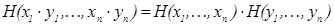
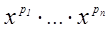 , x>0
, x>0
Доказательство. 1. Найдём все непрерывные хотя бы в одной точке решения уравнения 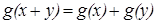 , которое будет основным, так как мы далее сведём к нему все остальные уравнения.
, которое будет основным, так как мы далее сведём к нему все остальные уравнения.
Зафиксируем точку х0 из области определения – ту самую, в которой решение непрерывно, и проверим верность равенства 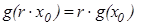 для любого r
для любого r 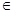 R.
R.
 , что возможно только при
, что возможно только при 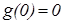 ;
;
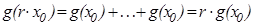 для любого r
для любого r 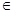 N;
N;
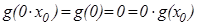 для r=0;
для r=0;
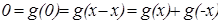 , но тогда
, но тогда 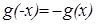 и
и 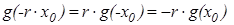 для любого r
для любого r 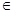 N, то есть равенство верно для всех целых r.
N, то есть равенство верно для всех целых r.
Далее пусть r 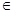 Q или r=z/n, где p
Q или r=z/n, где p 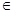 Z и q
Z и q 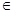 N.
N. 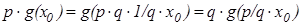 и поэтому
и поэтому 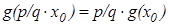 , то есть равенство верно для всех рациональных r.
, то есть равенство верно для всех рациональных r.
На последнем шаге используем непрерывность решения в точке х0 и тот факт, что любое действительное число представляется как предел некоторой рациональной последовательности.
Если 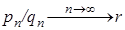 , то
, то 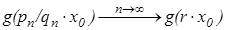 и
и  , а так как
, а так как 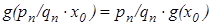 , заключаем, что
, заключаем, что 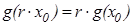 для любого r
для любого r 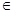 R.
R.
Теперь 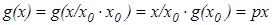 , p
, p 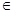 R (если обозначить не зависящий от х множитель
R (если обозначить не зависящий от х множитель 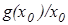 за p).
за p).
2. Рассмотрим уравнение 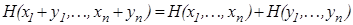 .
.
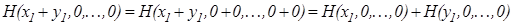 , и поэтому функция
, и поэтому функция  , непрерывная хотя бы в одной точке, удовлетворяет уравнению
, непрерывная хотя бы в одной точке, удовлетворяет уравнению 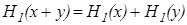 , то есть уравнению 1, и поэтому
, то есть уравнению 1, и поэтому 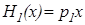 .
.
Точно так же  , …,
, …, 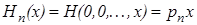 . Но искомое решение
. Но искомое решение 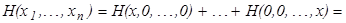
 , pi
, pi 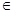 R.
R.
3. Решим уравнение 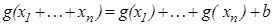 .
.
 , откуда
, откуда 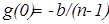 , и поэтому функция
, и поэтому функция 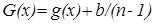 , непрерывная хотя бы в одной точке, удовлетворяет уравнению
, непрерывная хотя бы в одной точке, удовлетворяет уравнению 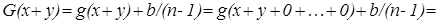
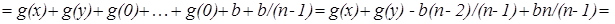
 , то есть
, то есть 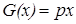 .
.
Тогда 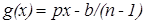 .
.
4. Обратимся к уравнению 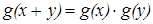 .
.
Прежде всего заметим, что если 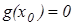 при каком-либо x0, то для любого x можно заключить
при каком-либо x0, то для любого x можно заключить 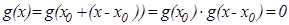 , то есть
, то есть 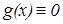 .
.
Это одно из решений уравнения, и если существует другое решение, то оно не обращается в нуль ни в одной точке. Тогда  . Но для положительной всюду
. Но для положительной всюду 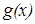 можно определить функцию
можно определить функцию 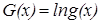 , которая непрерывна хотя бы в одной точке и удовлетворяет уравнению
, которая непрерывна хотя бы в одной точке и удовлетворяет уравнению
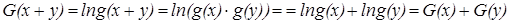 , то есть
, то есть 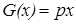 . Откуда
. Откуда 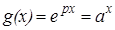 , где
, где  .
.
5. Рассмотрим уравнение 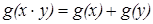 .
.
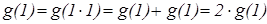 , и поэтому
, и поэтому 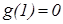
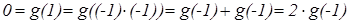 , и поэтому
, и поэтому 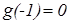
 , то есть g(x) – чётная функция.
, то есть g(x) – чётная функция.
Очевидно, если g(x)≠0, то она не определена при х=0. Действительно, если существует g(0), то 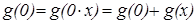 , откуда
, откуда 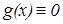 – тривиальное решение,существование которого очевидно.Таким образом уравнение достаточно рассматривать при х>0, а на отрицательную полуось решение продолжить чётным образом.
– тривиальное решение,существование которого очевидно.Таким образом уравнение достаточно рассматривать при х>0, а на отрицательную полуось решение продолжить чётным образом.
Определим функцию 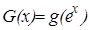 , где
, где 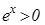 для любого х. G(x) непрерывна хотя бы в одной точке и удовлетворяет уравнению
для любого х. G(x) непрерывна хотя бы в одной точке и удовлетворяет уравнению 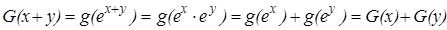 , то есть
, то есть 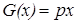 . Откуда
. Откуда  , где
, где 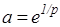 . И с учётом чётного продолжения
. И с учётом чётного продолжения 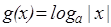 .
.
6. Уравнение 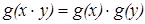 также сведём к уравнению 1.
также сведём к уравнению 1.
Прежде всего заметим, что если 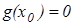 при каком-либо
при каком-либо 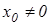 , то для любого x можно заключить
, то для любого x можно заключить  , то есть
, то есть 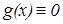 –тривиальное решение. Далее
–тривиальное решение. Далее 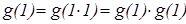 , и так как
, и так как 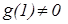 длянетривиального решения, то из этого равенства следует, что
длянетривиального решения, то из этого равенства следует, что 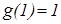 .
.
Но тогда 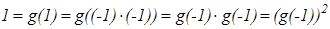 и g(–1)=
и g(–1)= 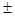 1.
1.
Если 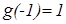 , то
, то 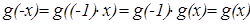 , и g(x) – чётная функция. Если же
, и g(x) – чётная функция. Если же 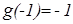 , то
, то 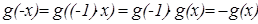 , и g(x) – нечётная функция. Таким образом g(x) достаточно найти при х>0, а на отрицательную полуось решение продолжить или чётным, или нечётным образом, получив тем самым два решения функционального уравнения.
, и g(x) – нечётная функция. Таким образом g(x) достаточно найти при х>0, а на отрицательную полуось решение продолжить или чётным, или нечётным образом, получив тем самым два решения функционального уравнения.
При х>0 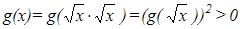 , так как
, так как  – мы ищем нетривиальное решение.Поэтомуможно определить функцию
– мы ищем нетривиальное решение.Поэтомуможно определить функцию 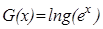 , которая непрерывна хотя бы в одной точке и удовлетворяет уравнению
, которая непрерывна хотя бы в одной точке и удовлетворяет уравнению 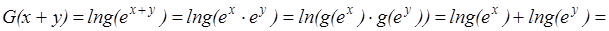
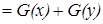 , то есть
, то есть 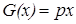 . Откуда
. Откуда 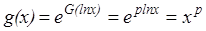 .
.
И с учётом чётного и нечётного продолжений имеем два решения 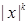 и
и 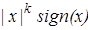 , x≠0. Для k>0 функции можно по непрерывности доопределить и в нуле, но для k<0 это сделать невозможно. Заметим, что при k=0 вторая функция есть
, x≠0. Для k>0 функции можно по непрерывности доопределить и в нуле, но для k<0 это сделать невозможно. Заметим, что при k=0 вторая функция есть  , и мы получаем пример разрывного решения.
, и мы получаем пример разрывного решения.
7. И уравнение 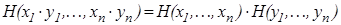 решим, используя предыдущее уравнение.
решим, используя предыдущее уравнение.
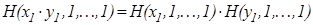 , и поэтому функция
, и поэтому функция 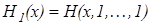 , непрерывная хотя бы в одной точке, удовлетворяет уравнению
, непрерывная хотя бы в одной точке, удовлетворяет уравнению 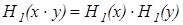 , но тогда по доказанному для x>0 имеем
, но тогда по доказанному для x>0 имеем 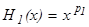 (в этом случае ограничимся положительными x, так как далее решение на всей числовой прямой нам не понадобится).
(в этом случае ограничимся положительными x, так как далее решение на всей числовой прямой нам не понадобится).
Аналогично, 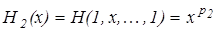 , …,
, …, 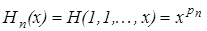 . Но искомое решение
. Но искомое решение 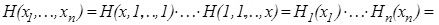
 , pi
, pi 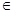 R.
R.
 2020-01-14
2020-01-14 104
104