Однородные квази-средние

Ранее мы говорили, что квази-средние в общем случае неоднородны, то есть соотношение 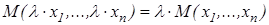для любых не выполняется, но их подкласс – взвешенные средние степенные 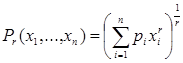обладают однородностью. Теперь покажем, что других квази-средних с данным свойством не существует [2].

Теорема 5. Взвешенные средние степенные – единственные однородные квази-средние.

Доказательство. Предположим, что равенство 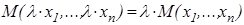имеет место, и выведем из него вид задающей квази-среднее функции . Перепишем 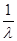или 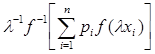= 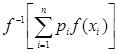. Получили тождественные квази-средние, заданные функциям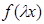и и . В силу теоремы 4 имеем 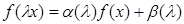(*), где 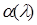и 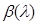– функции от λ, ≠ 0. Также мы можем положить .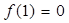

Тогда 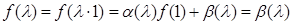. Подставляя теперь 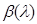в (*) и заменяя λ на y, найдём, что 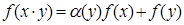(**). Аналогично .

Последние два равенства дают для x, y≠1 (***).

Отсюда следует, что функции в левой и правой частях (***) равны постоянной d, то есть .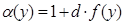

Из (**) вытекает сейчас равенство 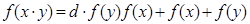, которое, очевидно, справедливо и для значений x=1 и y=1, и поэтому ограничение на (***) несущественно.

Итак, мы получили функциональное уравнение 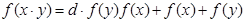, рассматривая его, различаем два случая:

1) при d=0 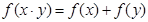, и поэтому для x>0 ;

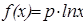2) при d ≠ 0 полагая 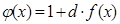, сведём уравнение к 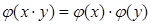, и поэтому для x>0 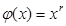и .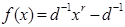

В первом случае по теореме 4 о тождественных квази-средних 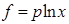можно заменить на 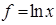, и тогдаполучаем среднее геометрическое, которое принято считать частным случаем среднего степенного при 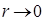. Во втором, заменяя 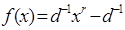на 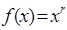– среднее степенное.