Квази-среднее  определено, если задана функция
определено, если задана функция  . Возникает естественный вопрос, справедливо ли обратное предложение: если
. Возникает естественный вопрос, справедливо ли обратное предложение: если  для любых
для любых  или
или  и
и  –тождественны, то следует ли отсюда, что задающие их функции
–тождественны, то следует ли отсюда, что задающие их функции  и
и  также тождественны. Ответ на этот вопрос даёт следующая
также тождественны. Ответ на этот вопрос даёт следующая
Теорема 4. Необходимым и достаточным условием тождественности квази-средних 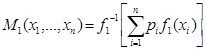 и
и  является условие
является условие  , где
, где  .
.
Доказательство. Если указанное условие выполняется, то

 , и поэтому
, и поэтому
 =
= 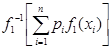 или
или  =
=  для любых
для любых  , то есть условие достаточно.
, то есть условие достаточно.
Обратно, пусть  =
=  ,
,  =
=  или
или  . Обозначая
. Обозначая  и
и  , перепишем
, перепишем  =
=  .
.
Сведём это равенство к функциональному уравнению. Возьмём точку  из области значений функции
из области значений функции  и представим
и представим  . Тогда
. Тогда  =
=  или
или  =
=  . Полагая
. Полагая  , где
, где  для каждого i, найдём
для каждого i, найдём 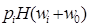 =
=  , где
, где  не зависит от
не зависит от  .
.
Поэтому  =
=  , что с обозначениями
, что с обозначениями 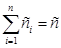 ,
,  ,
,  перепишется так:
перепишется так:  .
.
Тогда решением этого функционального уравнения будет функция 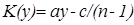 ,
,  , где
, где  . Так как
. Так как  , то
, то  ,или
,или  , если взять
, если взять  .
.
Таким образом, чтобы задать одно и то же квази-среднее  мы можем взять любую функцию из целого класса функций
мы можем взять любую функцию из целого класса функций  , где а≠0 и b – произвольныепостоянные, и другого способа получить тождественные квази-средние не существует.
, где а≠0 и b – произвольныепостоянные, и другого способа получить тождественные квази-средние не существует.
 2020-01-14
2020-01-14 135
135








