Основные свойства верхнего центрального показателя

Р.Э. Виноград ввел[5] понятие верхнего центрального показателя системы

. (1)

Переход от невозмущенной системы (1) к возмущенной системе

сопровождается изменением показателей. Верхний центральный показатель системы (1) и характеризует это изменение в определенном классе возмущений. Имеет место теорема Р.Э. Винограда.

Теорема [2,с.164-166;3]. Для любого можно указать , что при любых непрерывных возмущениях ,

будут выполняться неравенства

В.В. Миллионщиковым доказано, что последняя оценка неулучшаема, а именно

Теорема [4]. Для любого найдется возмущение

Q_e , ||Q_e|| ,

такое, что система

Q_e

имеет решение , для которой

Значит, для рассмотренной в дипломной работе системы наиболее быстро растущими решениями «руководит» показатель , а не показатель .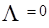

ЗАКЛЮЧЕНИЕ

В данной дипломной работе рассматриваются соотношения между старшим и верхним центральным показателями линейной системы

с кусочно непрерывными ограниченными коэффициентами.

Показано, что существует два различных случая отношений между старшим и верхним центральным показателями линейных систем: . На примере заданной линейной однородной диагональной системы дифференциальных уравнений подробно рассмотрены вычисления характеристического показателя Ляпунова, спектра, старшего и верхнего центрального показателей.