Независимые испытания с несколькими исходами

Рассмотрим схему независимых испытаний уже не с двумя, а с большим количеством возможных результатов в каждом испытании.

Пример 1. Игральная кость подбрасывается 15 раз. Найти вероятность того, что выпадет ровно десять троек и три единицы.

Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани. Поэтому воспользоваться формулой для числа успехов в схеме Бернулли не удаcтся.

Попробуем вывести подходящую формулу. Пусть в одном испытании возможны исходов: , и -й исход в одном испытании случается с вероятностью , где .

Обозначим через вероятность того, что в независимых испытаниях первый исход случится раз, второй исход - раз, и т.д., наконец, -й исход - раз.

Теорема 4 (Обобщенная формула Бернулли). Для любого и любых неотрицательных целых чисел сумма которых равна верна формула

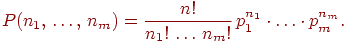
Доказательство. Рассмотрим один элементарный исход, благоприятствующий выпадению единиц, двоек и т.д.:

Это результат экспериментов, когда все нужные исходы появились в некотором заранее заданном порядке. Вероятность такого результата равна произведению вероятностей . Остальные благоприятные исходы отличаются лишь расположением чисел на местах. Число таких исходов равно числу способов расположить на местах единиц, двоек, и т.д. Это число равно