Отношение площадей подобных треугольников

Теорема 1. Площади двух треугольников, имеющих по равному углу, относятся, как произведения сторон, заключающих эти углы.

Доказательство. Пусть в треугольниках АВС и 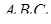 (рис. 1.43) углы А и  равны.

Рис. 1.43

Проведя высоты  и , будем иметь:

.

 

Треугольник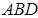и  и  подобны (Ð А = Ð А ₁ и Ð D = Ð D ₁ = =90⁰), поэтому 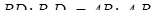; заменив первое отношение вторым, получим:

 

.

Теорема 2. Площади подобных многоугольников относятся как квадраты сходственных сторон.

Доказательство. 1) Если  и  - два подобных треугольника, то углы одного равны соответственно углам другого; пусть

 

Ð А = Ð А ₁, Ð В= = Ð В ₁, Ð С = Ð С ₁.

 

Применим к ним предыдущую теорему:

 

.                   (1.14)

 

Но из подобия треугольников следует:

 

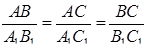                              (1.15)

 

Поэтому в равенстве (1.14) мы можем каждое из отношений  и  заменить любым отношением ряда (1.15), следовательно,

.

 

2) Если  и  (рис. 1.44) – два подобных многоугольника, то их можно разложить на одинаковое число подобных и одинаково расположенных треугольников.

 

Рис. 1.44

 

Пусть эти треугольники будут:

 

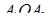 и 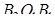,  и , …,  и .

 

Согласно доказанному в первой части этой теоремы, получим пропорции:

 

 …; .

 

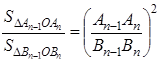Но из подобия многоугольников следует:

 

.

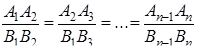И поэтому

 

.

 

Значит,

 

,

 

откуда

 

,

Следствие. Площади правильных одноимённых многоугольников относятся как квадраты сторон, или как квадраты радиусов апофем.

 

Фигуры с наибольшей площадью