Дано:
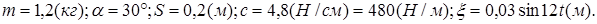
Найти: Уравнение движения
Решение:
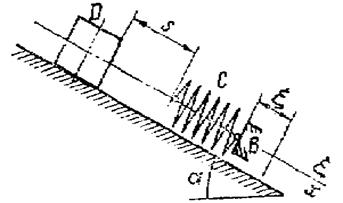
Применим к решению задачи дифференциальное уравнение движения точки. Совместим начало координатной системы с положением покоя груза, соответствующим статической деформации пружины, при условии что точка В занимает свое среднее положение 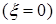 . Направим ось
. Направим ось 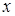 вниз вдоль наклонной плоскости. Движение груза определяется по следующему дифференциальному уравнению:
вниз вдоль наклонной плоскости. Движение груза определяется по следующему дифференциальному уравнению:
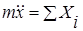 ,
,
где 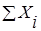 -сумма проекций на ось
-сумма проекций на ось 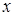 сил, действующих на груз.
сил, действующих на груз.
Таким образом
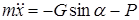
Здесь 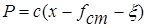 ,
,
где 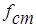 - статическая деформация пружины под действием груза;
- статическая деформация пружины под действием груза; 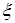 -перемещение точки прикрепления нижнего конца пружины, происходящее по закону
-перемещение точки прикрепления нижнего конца пружины, происходящее по закону 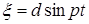
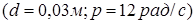 .
.
Статическую деформацию пружины 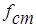 найдем из уравнения, соответствующего состоянию покоя груза:
найдем из уравнения, соответствующего состоянию покоя груза:
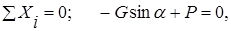
т.е. 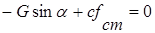
Откуда 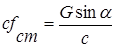
Дифференциальное уравнение движения груза примет вид:
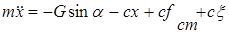
или после преобразования
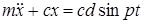
Разделив все члены уравнения на 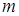 получим:
получим:
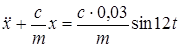
Введем обозначения:
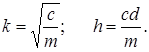
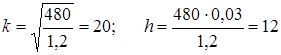
Получаем, что 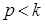
Имеем неоднородное уравнение
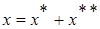 ,
,
где 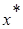 - общее решение, соответствующего однородного уравнения;
- общее решение, соответствующего однородного уравнения;
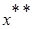 - частное решение данного неоднородного уравнения.
- частное решение данного неоднородного уравнения.
Общее решение однородного уравнения имеет вид:
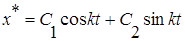
Частное решение неоднородного уравнения:
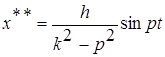
Общий интеграл
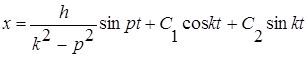
Для определения постоянных интегрирования найдем, кроме ого, уравнение для 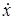 :
:
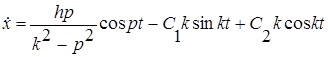
и используем начальные условия задачи.
Рассматриваемое движение начинается в момент 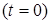 , когда деформация пружины является статической деформацией под действием груза.
, когда деформация пружины является статической деформацией под действием груза.
Таким образом, при 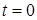
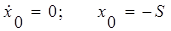
Составим уравнения 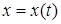 и
и 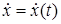 для
для 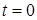 :
:
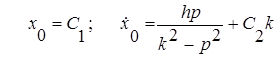
Откуда 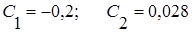
Тогда уравнение движения груза примет вид:
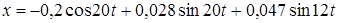
Ответ: 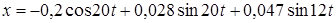
Применение теоремы об изменении количества движения к исследованию движения механической системы.
Дано:
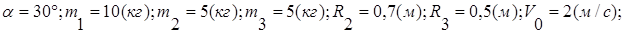
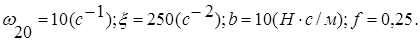
Найти: Скорость 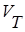 .
.
Решение:
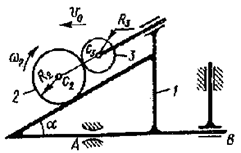
На механическую систему действуют внешние силы: 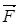 - сила сухого трения в опоре А;
- сила сухого трения в опоре А; 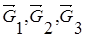 - силы тяжести тел 1, 2 и 3;
- силы тяжести тел 1, 2 и 3; 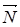 -сила нормальной реакции в точке А;
-сила нормальной реакции в точке А; 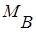 -реактивный момент в опоре В.
-реактивный момент в опоре В.
Применим теорему об изменении количества движения механической системы в дифференциальной форме. В проекциях на оси координат
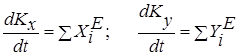 , (1)
, (1)
где 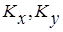 - проекции вектора количества движения системы на оси координат;
- проекции вектора количества движения системы на оси координат; 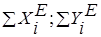 - суммы проекций внешних сил на соответствующие оси.
- суммы проекций внешних сил на соответствующие оси.
Количество движения системы тел 1, 2 и 3
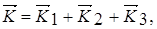 (2)
(2)
где 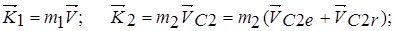
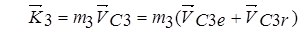 . (3)
. (3)
Здесь 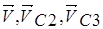 - скорости центров масс тел 1, 2, 3;
- скорости центров масс тел 1, 2, 3; 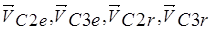 - соответственно переносные и относительные скорости центров масс.
- соответственно переносные и относительные скорости центров масс.
Очевидно, что
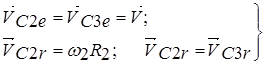 (4)
(4)
Проецируя обе части векторного равенства (2) на координатные оси, получаем с учетом (3) и (4)
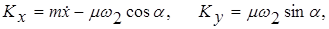 (5)
(5)
где 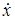 - проекция вектора
- проекция вектора 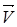 на ось
на ось 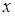 ;
;
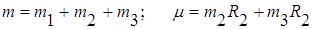
Проекция главного вектора внешних сил на координатные оси
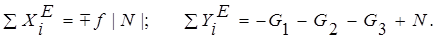 (6)
(6)
Знак «-» соответствует случаю, когда 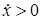 , а знак «+» - случаю, когда
, а знак «+» - случаю, когда 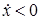 .
.
Подставляя (5) и (6) в (1), получим
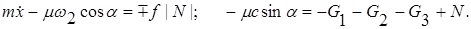 (7)
(7)
Выразим из второго уравнения системы (7) величину нормальной реакции и подставим ее в первое уравнение. В результате получим
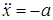 при
при 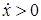 ; (8)
; (8)
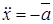 при
при 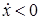 . (9)
. (9)
где
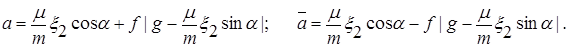
Рассмотрим промежуток времени 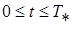 , в течении которого тело 1 движется вправо
, в течении которого тело 1 движется вправо 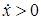 . Из (8) следует, что
. Из (8) следует, что
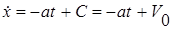 ,
,
где С- постоянная интегрирования, определяемая из начального условия: при 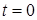
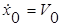 .
.
При 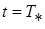 скорость тела 1 обращается в ноль, поэтому
скорость тела 1 обращается в ноль, поэтому 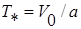 .
.
Найдем значения 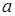 и
и 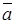 :
:
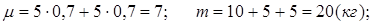
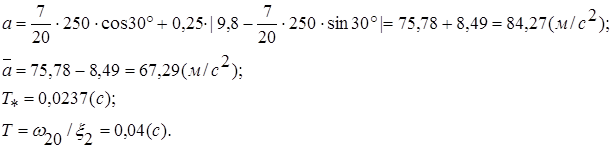
Т.е. 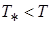 ,
, 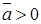 . Значит, тело при
. Значит, тело при 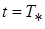 начинает двигаться в обратном направлении. Это движение описывается дифференциальным уравнением (9) при начальном условии:
начинает двигаться в обратном направлении. Это движение описывается дифференциальным уравнением (9) при начальном условии: 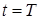 ;
; 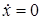 (10)
(10)
Интегрируя (9) с учетом (10), получим, при 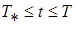
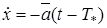 (11)
(11)
При 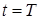 получим из (11) искомое значение скорости тела 1 в момент, когда
получим из (11) искомое значение скорости тела 1 в момент, когда
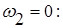
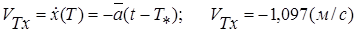 .
.
Точное решение задачи. Воспользовавшись методикой, изложенной выше, получим дифференциальное уравнение движения тела 1:
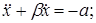 при
при 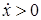 (12)
(12)
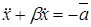 ; при
; при 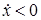 , (13)
, (13)
где 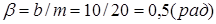
Из (12) и учитывая, что 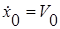 получаем, при
получаем, при 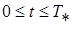
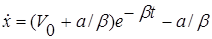
откуда 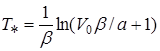 или
или 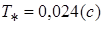
Из (13) и учитывая, что 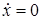 получаем, при
получаем, при 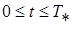
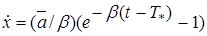
При 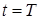 находим
находим
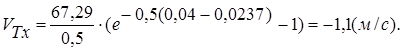
Ответ: 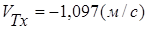
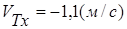 .
.
 2020-01-14
2020-01-14 458
458







