Формально-кинетические закономерности восстановления газами

Количественный анализ кинетических закономерностей топохимических реакций восстановления очень сложен. Теоретическое описание кинетики процесса восстановления для получения математической модели с перспективой внедрения ее в промышленную автоматизации разрабатывалось рядом ученых: Стальхане, Мальмберг, Любан, Манчинский и др. Наиболее полное решение было сделано Ростовцевым С.Т. в виде диффузионно-кинетической теории восстановления. При этом получились очень громоздкие уравнения, требующие для их количественного анализа ряда трудно определяемых из практики процессов параметров.

В данном разделе рассматриваются несколько идеализированных случаев восстановления, позволяющих с определенными приближениями к реальным процессам выяснить влияние ряда факторов на кинетику реакций.

 

Если процесс не лимитируется сложной в кинетическом описании кристаллохимической стадией зарождения новой фазы, то обратимую реакцию восстановления можно представить схемой

Скорость ее равна: ,                                      (44)

где  и  – константы скорости прямой и обратной реакций.

Так как общее давление газа ,

то

При равновесии или

где  – равновесное давление восстановителя.

Обозначив имеем                          (45)

Полученное уравнение показывает, что скорость процесса определяется величиной реакционной поверхностью, температурой и давлением газа на реакционной поверхности.

Если диффузия газа к поверхности реакционной не затруднена (кинетический режим), то ,где 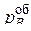– парциальное давление газа-восстановителя в объеме реактора, и уравнение (45) принимает вид:

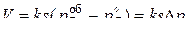                                              (46)

Следует отметить, что при более строгом выводе данного уравнения с учетом адсорбционно-десорбционных явлений, получаются более сложные зависимости.

 

Если исходный оксид состоит из частиц сферической формы с начальным радиусом   и имеет массу , то к моменту времени t произойдет изменение массы  и радиуса 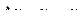, где m и r – масса материала и радиус частиц к моменту времени t. Тогда степень восстановления α исходного оксида . Для каждой из частиц , где – плотность вещества. Подставляя m и  в выражение для , получаем

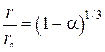.                           (47)

Скорость процесса V, выраженная через изменение количества (моль) исходного вещества в единицу времени

           (48)

где M – молярная масса вещества.

Сравнивая полученное выражение с уравнением (46) для скорости процесса в кинетическом режиме и учитывая в последнем , получим

 и .           (49)

При постоянных значениях температуры и давления, значит, k и 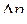, а также молярного объема  скорость уменьшения размера непрореагировавшей части исходного оксида постоянна, то есть . После интегрирования этого уравнения от 0 до t и от  до r получаем . Отсюда относительная толщина слоя продукта

.

Записав отношение размера непрореагировавшей части исходного оксида к начальному размеру через степень восстановления приходим к уравнению

.                                      (50)

Это уравнение, приведенное к форме

,                                             (51)

известно как закономерность модели сжимающегося объема или как уравнение Мак-Кевана. Оно предполагает быстрое образование границы раздела фаз с последующим линейным во времени продвижением реакционной зоны в объем сферического зерна.

Для полного завершении восстановления () требуется время

.                                  (52)

Оно, как видно, уменьшается с уменьшением размера частиц материала, с ростом температуры, что соответствует увеличению константы скорости, с увеличением фактического парциального давления газа-восстановителя в объеме реактора, что соответствует увеличению .

 

Если в процессе восстановления продукт оказывается малопористым, плотным, то имеются значительные диффузионные торможения, и процесс может осуществляться в диффузионном режиме. Адсорбционно – кристаллохимические реакции идут быстро, и поэтому в порах на границе раздела фаз устанавливается давление, близкое к равновесному , и соответствующая ему концентрация газа .

На наружной поверхности частично прореагировавшего зерна устанавливается концентрация , соответствующая давлению  в объеме газа при отсутствии внешнедиффузионных торможений.

Скорость диффузии газа через слой оксида в соответствии с законом Фика

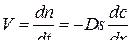.                                               (53)

Для процесса со сферической формой частиц

,                                  (54)

где – радиус сферы в слое оксида, изменяющийся от  до r за время t.

При решении этого уравнения возможны несколько различных допущений. В первом приближении для квазистационарного процесса градиент концентрации 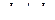 может быть заменен отношением приращений .

Тогда                       .                                       (55)

Введя в данное выражение скорость из выражения (48) получим

             (56)

Отсюда следует, что линейная скорость обратно пропорциональна толщине оксидного слоя. Разделим переменные и проинтегрируем

.

Тогда                                ,                                      (57)

то есть толщина слоя изменяется во времени по параболическому закону . Введя  из выражения  (47), получим уравнение

,                                         (58)

которое известно как уравнение Яндера.

Оно является приближенным для частиц сферической формы, так как связь толщины слоя с радиусом непрореагировавшей части частицы малого размера оказывается более сложной.

Учет изменения объема сферы по ходу реакции может быть выполнен следующим образом. Уравнение (54) перепишем в виде . Интегрируя в приближении независимости скорости диффузионного потока от x

,

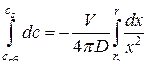получаем  или .                       (59)

Сопоставление уравнений (59) и (48) дает выражение для линейной скорости перемещения реакционной зоны

,                           (60)

из которого видна более сложная, чем из выражения (56) зависимость линейной скорости от размера r непрореагировавшей части оксида. На начальном этапе, когда 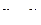 сферическая симметрия частиц не проявляется, то есть линейная скорость, как и в предыдущем случае, обратно пропорциональна толщине оксидного слоя (). Затем при  с дальнейшим утолщением слоя продукта диссоциации (с уменьшением r) линейная скорость возрастает.

Интегрирование уравнения (60) и введение степени превращения  через отношение (47) приводит к кинетическому уравнению

.                 (61)

Приведенное к форме

,                                    (62)

оно известно как уравнение Кранка, Гистлинга и Браунштейна.

Из уравнения (61) время полного завершения восстановления оксида ()

.                                                   (63)

Сравнение с уравнением (52) для времени завершения процесса в кинетическом режиме приводит качественно к тем же выводам. Однако для процесса в диффузионном режиме следует отметить более сильное влияние размера зерен оксида и менее сильное влияние температуры, так как к сильному уменьшению  за счет экспоненциального роста  с ростом температуры добавляется некоторое увеличение с ростом величины T, находящейся в числителе уравнения (63).