2020-01-14
92
Перепишем условие мат. Модели таким образом, чтоб все ограничения задачи имели один знак. Для классической задачи МАКСИМУМ, знак ограничений должен быть типа «≤»
Для того что б последние 3 неравенства были такие как нам надо, домножаем их на «-1»
Перейдем к каноническому виду, для этого необходимо от неравенств-ограничений перейти к ограничениям-равенствам. Вводим дополнительные переменные. Так как все неравенства типа «≤», то дополнительные переменные вводим со знаком «+»
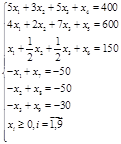
х1, х2, х3- свободные переменные
х4, х5, х6, х7, х8, х9- базисные переменные
Составим и заполним 1-ую симплексную таблицу
|
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A4 | 0 | 400 | 5 | 3 | 5 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | A5 | 0 | 600 | 4 | 2 | 7 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | A6 | 0 | 150 | 1 | 1/2 | 1/3 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | A7 | 0 | -50 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | A8 | 0 | -50 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A9 | 0 | -30 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 0 | -25 | -20 | -50 | 0 | 0 | 0 | 0 | 0 | 0 | ||
Находим пробное решение, для этого все свободные переменные приравниваем к 0, а базисные к bi
|
|
|
| Свободные переменные | Базисные переменные |
| X1=0 X2=0 X3=0 | X4=400 X5=600 X6=150 X7=-50 X8=-50 X9=-30 |
Решение пробное.
Но так как в столбце bi есть отрицательные коэффициенты, то решение не ОПОРНОЕ.
Для решение задачи двойственным симплекс методом для начала необходимо добиться, что б решение было ОПОРНЫМ.
Находим в столбце Bi минимальный отрицательный коэффициент.
Bi=min{bi<0}=min{-50;-50;-30}= -50
Соответствует сразу двум строкам А7 и А8. Одна из этих строк будет разрешающей.
Для того что б определиться какую из двух строк выбрать в качестве разрешающей, для каждой найдем разрешающий столбец, а затем проверим при замене какой пары (разрешающая строка + разрешающий столбец) изменение функции цели будет больше (ту пару и будем менять)
1) А7- разрешающая строка
Ищем разрешающий столбец по правилу:
(так как среди оценочной строки имеются отрицательные оценки плана (задача максимизации), то среди отрицательных коэффициентов аij разрешающей строки выбирается разрешающий элемент аrs для которого
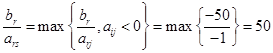соответствует столбцу А1
Если заменим А1—А7 то функция цели изменится на:
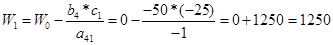
2) А8- разрешающая строка
соответствует столбцу А2
Если заменим А2—А8 то функция цели изменится на:
В первом случае изменение функции больше, поэтому выбираем пару А1-А7 меняем вектора местами и переходим к новой симплекс-таблице по правилу:
Переходим к новой симплекс таблице по следующему правилу:
1. все элементы разрешающей строки делим на разрешающий элемент
2. заполняем базисные столбцы
|
|
|
3. все остальные элементы симплекс таблицы находим по формуле:
|
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A4 | 0 | 150 | 0 | 3 | 5 | 1 | 0 | 0 | 5 | 0 | 0 |
| 2 | A5 | 0 | 400 | 0 | 2 | 7 | 0 | 1 | 0 | 4 | 0 | 0 |
| 3 | A6 | 0 | 100 | 0 | 1/2 | 1/3 | 0 | 0 | 1 | 1 | 0 | 0 |
| 4 | A1 | 25 | 50 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 |
| 5 | A8 | 0 | -50 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A9 | 0 | -30 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 1250 | 0 | -20 | -50 | 0 | 0 | 0 | -25 | 0 | 0 | ||
Новое решение
| Свободные переменные | Базисные переменные |
| X2=0 X3=0 X7=0 | X1=50 X4=150 X5=400 X6=100 X8=-50 X9=-30 |
Решение все еще не опорное, так как все еще есть bi<0
Находим разрешающую строку:
Bi=min{bi<0}=min{-50;-30}= -50
Соответствует строке А8
Разрешающий столбец:
соответствует столбцу А2
Меняем А2—А8
Переходим к новой симплекс таблице:
|
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A4 | 0 | 0 | 0 | 0 | 5 | 1 | 0 | 0 | 5 | 3 | 0 |
| 2 | A5 | 0 | 300 | 0 | 0 | 7 | 0 | 1 | 0 | 4 | 2 | 0 |
| 3 | A6 | 0 | 75 | 0 | 0 | 1/3 | 0 | 0 | 1 | 1 | 1/2 | 0 |
| 4 | A1 | 25 | 50 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 |
| 5 | A2 | 20 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 0 |
| 6 | A9 | 0 | -30 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 2250 | 0 | 0 | -50 | 0 | 0 | 0 | -25 | -20 | 0 | ||
Новое решение
| Свободные переменные | Базисные переменные |
| X3=0 X7=0 X8=0 | X1=50 X2=50 X4=0 X5=300 X6=75 X9=-30 |
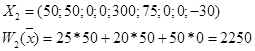
Решение все еще не опорное, так как все еще есть bi<0
В качестве разрешающей строки берем А9
Разрешающий столбец А3
Меняем А3—А9
|
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A4 | 0 | -150 | 0 | 0 | 0 | 1 | 0 | 0 | 5 | 3 | 5 |
| 2 | A5 | 0 | 90 | 0 | 0 | 0 | 0 | 1 | 0 | 4 | 2 | 7 |
| 3 | A6 | 0 | 65 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1/2 | 1/3 |
| 4 | A1 | 25 | 50 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 |
| 5 | A8 | 20 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 0 |
| 6 | A9 | 0 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | -1 |
| ∆j=W(j)-cj | 2400 | 0 | 0 | 0 | 0 | 0 | 0 | -25 | -20 | -50 | ||
Новое решение
| Свободные переменные | Базисные переменные |
| X9=0 X7=0 X8=0 | X1=50 X2=50 X3=30 X4= -150 X5=90 X6=65 |
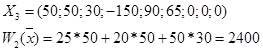
Решение все еще не опорное, так как все еще есть bi<0
В строке №1 появился отрицательный коэффициент -150. Берем в качестве разрешающей строки строку №1.
Так как в строке №1 нет ни одного отрицательного коэффициента то решения НЕТ!
Возможно в условии задачи вместо МИНИМАЛЬНОГО спроса имели ввиду МАКСИМАЛЬНЫЙ.
Решим задачу для условия, что максимальный спрос на изделия составляет 50, 50 и 30единиц.
Тогда математическая модель задачи:
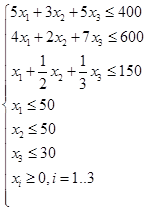
Канонический вид задачи линейного программирования:
х1, х2, х3- свободные переменные
х4, х5, х6, х7, х8, х9- базисные переменные
Составим и заполним 1-ую симплексную таблицу для нового условия задачи:
|
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A4 | 0 | 400 | 5 | 3 | 5 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | A5 | 0 | 600 | 4 | 2 | 7 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | A6 | 0 | 150 | 1 | 1/2 | 1/3 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | A7 | 0 | 50 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | A8 | 0 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A9 | 0 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 0 | -25 | -20 | -50 | 0 | 0 | 0 | 0 | 0 | 0 | ||
Находим пробное решение, для этого все свободные переменные приравниваем к 0, а базисные к bi
| Свободные переменные | Базисные переменные |
| X1=0 X2=0 X3=0 | X4=400 X5=600 X6=150 X7=50 X8=50 X9=30 |
Решение ОПОРНОЕ, так как все коэффициенты в столбце bi>=0.
Для того что бы задача МАКСИМУМ имела оптимальное решение, необходимо, что б все коэффициенты в строке функции цели ∆j=W(j)-cj были не отрицательные (∆j≥0). У нас в этой строке есть отрицательные коэффициенты, поэтому решение НЕ ОПТИМАЛЬНОЕ.
Всего у нас три столбца у которых оценка плана отрицательна А1, А2 и А3.
Рассмотрим каждый из них и выберем тот который более выгодно ввести в базис. (Другими слова, при вводе какого вектора функция цели будет иметь наибольшее изменение)
А1 столбец:
Функция цели меняется по формуле:
Для столбца А1: 
Тогда 
Если будем вводить вектор А1, то функция цели увеличится на 1250 единиц
|
|
|
=0-(-1250)=1250
А2 стролбец:
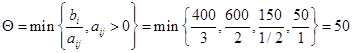
Функция цели меняется по формуле:
Для столбца А2: 
=-20
Тогда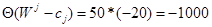 
Если будем вводить вектор А2, то функция цели увеличится на 1000 единиц
=0-(-1000)=1000
А3 столбец:
Функция цели меняется по формуле:
Для столбца А3: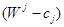 
=-50
Тогда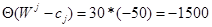 
Если будем вводить вектор А3, то функция цели увеличится на 1500 единиц
=0-(-1500)=1500
Больше всего функция цели увеличится, если введем вектор А3.
Поэтому А3 – разрешающий столбец
Находим разрешающую строку по правилу:
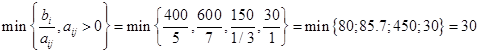
соответствует строке 6 и вектору А9
Меняем А3—A9
|
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A4 | 0 | 250 | 5 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | -5 |
| 2 | A5 | 0 | 390 | 4 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | -7 |
| 3 | A6 | 0 | 140 | 1 | 1/2 | 0 | 0 | 0 | 1 | 0 | 0 | -1/3 |
| 4 | A7 | 0 | 50 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | A8 | 0 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A3 | 50 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 1500 | -25 | -20 | 0 | 0 | 0 | 0 | 0 | 0 | 50 | ||
Новое решение
| Свободные переменные | Базисные переменные |
| X1=0 X2=0 X9=0 | X3=30 X4=250 X5=390 X6=140 X7=50 X8=50 |
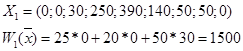
Решение опорное, но пока еще не оптимальное, так как есть отрицательные коэффициенты в строке функции цели.
Так как в двух столбцах оценка плана отрицательна рассмотрим изменение функции цели при вводе этих столбцов в базис:
А1 столбец:
Функция цели меняется по формуле:
Для столбца А1: 
Тогда 
Если будем вводить вектор А1, то функция цели увеличится на 1250 единиц
=1500-(-1250)=2750
А2 стролбец:
Функция цели меняется по формуле:
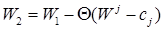
Для столбца А2: 
=-20
Тогда 
Если будем вводить вектор А2, то функция цели увеличится на 1000 единиц
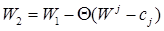=1500-(-1000)=2500
Выгоднее вводить вектор А1, так как изменение функции цели в этом случае больше.
Разрешающий столбец А1
Ищем разрешающую строку:
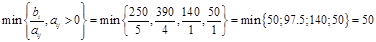
соответствует строке 1и 5 (векторам А4 и А8)
Возьмем в качестве разрешающей строки строку №1 и вектор А4
Меняем А4 и А8
|
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||||
| 1 | A1 | 25 | 50 | 1 | 0,6 | 0 | 0,2 | 0 | 0 | 0 | 0 | -1 | ||
| 2 | A5 | 0 | 190 | 0 | -0.4 | 0 | -0,8 | 1 | 0 | 0 | 0 | -3 | ||
| 3 | A6 | 0 | 90 | 0 | -0.1 | 0 | -0,2 | 0 | 1 | 0 | 0 | 2/3 | ||
| 4 | A7 | 0 | 0 | 0 | -0.6 | 0 | -0,2 | 0 | 0 | 1 | 0 | 1 | ||
| 5 | A8 | 0 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| 6 | A3 | 50 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| ∆j=W(j)-cj
| 2750 | 0 | -5 | 0 | 5 | 0 | 0 | 0 | 0 | 25 | ||||
Находим пробное решение, для этого все свободные переменные приравниваем к 0, а базисные к bi
| Свободные переменные | Базисные переменные |
| X2=0 X4=0 X9=0 | X1=50 X3=30 X5=190 X6=90 X7=0 X8=50 |
Решение опорное, но не оптимальное.
Разрешающий столбец № 2 (вектор А2 так как только у него есть отрицательная оценка плана)
Найдем разрешающий столбец:
| БП | C1=25 | С2=20 | C3=50 | C4=0 | C5=0 | C6=0 | C7=0 | C8=0 | C9=0 | ||
| Сб | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A1 | 25 | 20 | 1 | 0 | 0 | 0,2 | 0 | 0 | 0 | -0,6 | -1 |
| 2 | A5 | 0 | 210 | 0 | 0 | 0 | -0,8 | 1 | 0 | 0 | 0.4 | -3 |
| 3 | A6 | 0 | 95 | 0 | 0 | 0 | -0,2 | 0 | 1 | 0 | 0,1 | 2/3 |
| 4 | A7 | 0 | 30 | 0 | 0 | 0 | -0,2 | 0 | 0 | 1 | 0.6 | 1 |
| 5 | A2 | 20 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A3 | 50 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 3000 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 5 | 25 | ||
соответствует строке №5 и вектору А8
Меняем А8—А5
Находим пробное решение, для этого все свободные переменные приравниваем к 0, а базисные к bi
| Свободные переменные | Базисные переменные |
| X4=0 X8=0 X9=0 | X1=20 X2=50 X3=30 X5=210 X6=95 X7=30 |
Решение ОПОРНОЕ и ОПТИМАЛЬНОЕ! Все коэффициенты в строке ∆j≥0
Для получения максимальной прибыли необходимо выпускать товар в следующем ассортименте:
Изделия 1-го типа в размере х1=20 шт
Изделия 2-го типа в размере х2=50шт
Изделия 3-го типа в размере х3=30шт
При таком выпуске получим максимальную прибыль в размере W*=3000$
