2020-01-14
120
Если дополнительная переменная i-го ограничения базисная, то ее значение дает диапазон изменения, в котором соответствующая компонента bi может уменьшаться (увеличиваться, если ограничение ≥)
Решение остается оптимальным в диапазоне:
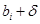где
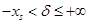для ограничения ≤
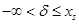для ограничения ≥
где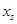 
-значение соответствующее дополнительной пересенной
1) Х5 в2=600
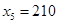ограничение ≤
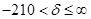
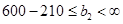
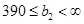
2) Х6 в3=150
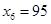
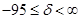
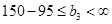
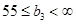
3) Х7 в4=50
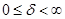
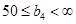
Небазисная дополнительная переменная: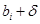
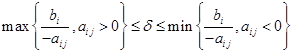
1) x4
b1=400
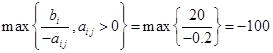
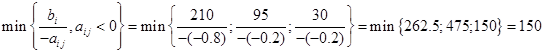
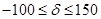
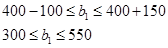
2) x8
b5=50
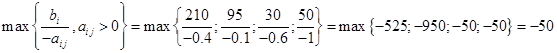
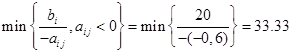
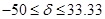
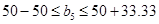
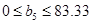
3) x9
b6=30
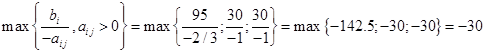
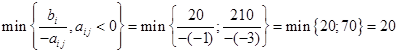
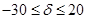
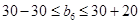
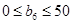
1) От итоговой симплекс-таблицы прямой задачи перейдем к решению двойственной.
Сформулируем двойственную задачу:
- Так как прямая задача- задача на максимум, то двойственная ей задача на минимум.
- Коэффициенты функции цели прямой задачи будут коэффициентами вектора ограничений для двойственной.
- Коэффициенты вектора ограничений прямой задачи будут коэффициентами функции цели для двойственной.
- Ограничения двойственной задачи будут иметь знак ≥
|
|
|
| Прямая задача |
|
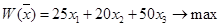
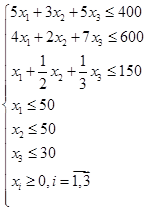
| Двойственная задача |
|
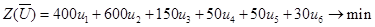
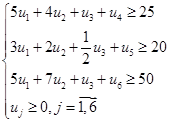
Для удобства перехода между прямой и двойственной задачами подпишем внутри последней симплекс-таблицы соответствующие переменные двойственной задачи
|
| БП | U7 | U8 | U9 | U1 | U2 | U3 | U4 | U5 | U6 | ||
| Двойств | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A1 | U7 | 20 | 1 | 0 | 0 | 0,2 | 0 | 0 | 0 | -0,6 | -1 |
| 2 | A5 | U2 | 210 | 0 | 0 | 0 | -0,8 | 1 | 0 | 0 | 0.4 | -3 |
| 3 | A6 | U3 | 95 | 0 | 0 | 0 | -0,2 | 0 | 1 | 0 | 0,1 | 2/3 |
| 4 | A7 | U4 | 30 | 0 | 0 | 0 | -0,2 | 0 | 0 | 1 | 0.6 | 1 |
| 5 | A2 | U8 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A3 | U9 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 3000 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 5 | 25 | ||
Итоговая симплекс-таблица двойственной задачи:
|
| БП | Сбаз | Вi | C1=400 | С2=600 | C3=150 | C4=50 | C5=50 | C6=30 | C7=0 | C8=0 | C9=0 |
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | ||||
| 1 | U1 | 400 | 5 | 1 | 0.8 | 0.2 | 0.2 | 0 | 0 | -0.2 | 0 | 0 |
| 2 | U5 | 50 | 5 | 0 | -0.4 | -0.1 | -0.6 | 1 | 0 | 0.6 | -1 | 0 |
| 3 | U6 | 30 | 25 | 0 | 3 | -2/3 | -1 | 0 | 1 | 1 | 0 | -1 |
| ∆j=Z(j)-cj | 0 | -210 | -95 | 30 | 0 | 0 | -20 | -50 | -30 | |||
Оптимальным решением двойственной задачи будет:
| Свободные переменные | Базисные переменные |
| U2=0 U3=0 U4=0 U7=0 U8=0 U9=0 | U1=5 U5=5 U6=25 |
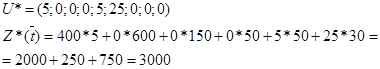
5) Целочисленное решение методом отсечения.
Так как в ходе решения нами было найдено целочисленное решение задачи максимум, то поставленная перед нами задача полностью решена!
Для получения максимальной прибыли рекомендуется выпускать изделия в следующем ассортименте:
Изделия Типа 1 в размере х1=20 шт
Изделия Типа 2 в размере х2=50 шт
Изделия Типа 3 в размере х3=30 шт
При таком выпуске прибыль будет максимальна и составит W*=3000 $
