Коэффициенты разложения нагрузки в ряд по синусам кратного аргумента

 (11)

 

При m=1,3,5….

Общий интеграл дифференциального уравнения, определяющего функцию f_m (у) (12) Выражение для прогиба пластины, свободно опертой по всем четырем кромкам и загруженной равномерно распределенным давлением (13).

 (12)

 

m=1,3,5...

Постоянные А_m и D_m, должны быть определены из граничных условий для функций f_m (у) при у = .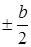

 (13)

 

Расчёт величины наибольшей стрелки прогиба в центре пластины.

Поскольку для рассматриваемой пластины , то по табл.1 находим

 

k₁=0,0843; k₂=0,0499; k₃=0,0812; k₄=0,242; k₅=0,424; k₆=0,320; k₇=0,486; k₈=0,057.

 =  (см) (14)

 

Расчёт величины изгибающих моментов М₁ в центре пластины в сечениях, перпендикулярных оси ох, и М₂ - в сечении, перпендикулярном оси оу.

 =  (15)

 

Расчёт величины наибольших значений перерезывающих сил по середине опорных кромок пластины, N₁ и N₂ (16).

 =  (16)

Расчёт величины наибольших значений реакций опорных кромок по их середине г₁ и r_{2 (}17).

 =  (17)

 

Расчёт величины напряжений изгиба пластины (18).

 = ,  =

 

Расчёт пластины, свободно опертой на кромках х=0 и х=а и жестко заделанной на кромках у = , при действии на пластину, равномерно распределена по всей ее площади. Расчётная схема (рис.4).

Рис.4

Выражение для функции .

 (19)

 

Входящие в это выражение постоянные интегрирования А_m и D_m, должны быть определены из условий для функций  при у = .

Граничные условия для функций

 (20)

 

Выражение для прогиба пластины свободно опертой на кромках х=0 и х=а и жестко заделанной на кромках у = .

 (21)

 

Расчёт величины стрелка прогиба в центре пластины (22).

Для рассматриваемой пластины длина жестко заделанных кромок больше, чем свободно опертых, поэтому коэффициенты должны определяться по столбцам левой части табл.2. Так как , то k₁ = 0,0582, k₂=0,0460, k₃=0,0585, k₄=0,1049.

 

 (22)

 

Расчёт величины изгибающих моментов в центре пластины (23).

Изгибающие моменты в центре пластины: М₁ - момент в сечении, перпендикулярном оси ох; М₂ - момент в сечении, перпендикулярном оси оу:

;

;

М₂= 0,0460·0,5·130² = 388,7 (кгс)

М₁= 0,0585·0,5·130² = 494,325 (кгс)

 

Расчёт величины изгибающих моментов по середине жестко заделанных кромок (24).

 

Расчёт величины напряжений изгиба в центре пластины и по середине жестко заделанных кромок (25).

 =

Изгиб пластин, жестко заделанных по всем четырем кромкам, при действии равномерно распределенной нагрузки. Расчётная схема (рис.5).

Рис.5