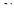Прежде всего, вычислим "точечный прогноз", рассчитываемый на основе полученного уравнения тренда:
уt = 17,73+0,1*16
уt = 19,33
Рассчитаем прогноз на основе доверительных интервалов. Доверительный интервал определяется по формуле:
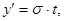
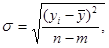
где  - отклонение от прогнозных значений;
- отклонение от прогнозных значений; 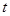 - коэффициент доверия (t =2);
- коэффициент доверия (t =2);  - среднее квадратическое отклонение;
- среднее квадратическое отклонение;  - уровни эмпирического ряда;
- уровни эмпирического ряда; 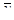 - средняя эмпирического ряда;
- средняя эмпирического ряда;  - число периодов;
- число периодов;  - число параметров уравнения (для прямой m =2).
- число параметров уравнения (для прямой m =2).
Найдем среднее квадратическое отклонение, для этого проведем вспомогательные расчеты, результаты отразим в таблице 2.3
Вспомогательные расчеты для определения доверительного интервала:
| Года | 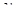
| yt - 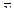
| (yt - 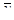 ) 2 ) 2
| ||||||||||||||||||||||||||||||
| 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 |
|
| 5,76 1,96 0,25 0,16 1,44 1,96 1 0,64 0,25 0,04 0,01 3,24 0,25 0,01 1,21 | ||||||||||||||||||||||||||||||
| Итого | 213,2 | 18,18 |
Найдем среднее квадратическое отклонение по рассчитанным данным:

Таким образом, можно рассчитать доверительный интервал. Примем t=2.
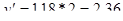
Интервальный прогноз учитывает отклонение эмпирических точек от теоретических.
Теперь рассчитаем среднюю ошибку:
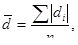
где 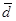 - среднее значение остатка;
- среднее значение остатка; 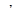 - остаток i-ого периода;
- остаток i-ого периода;  - число периодов. Найдем теоретические значения уровней ряда (аналогично нахождению значения "точечного прогноза"). Рассчитаем разность теоретического значения уровня ряда и средней арифметической простой эмпирического ряда, для нахождения среднего квадратического отклонения (средняя арифметическая равна а0). Результаты поместим в таблице 2.4
- число периодов. Найдем теоретические значения уровней ряда (аналогично нахождению значения "точечного прогноза"). Рассчитаем разность теоретического значения уровня ряда и средней арифметической простой эмпирического ряда, для нахождения среднего квадратического отклонения (средняя арифметическая равна а0). Результаты поместим в таблице 2.4
Для определения среднего остатка построим вспомогательную таблицу:
Таблица 2.4 Расчет среднего остатка для средней ошибки
| Года |
| yt | d=y - yt | ||||
| 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 | 16,5 16,8 17,1 17,4 17,7 18,0 18,0 18,0 18,1 18,1 18,1 18,1 18,0 17,9 | 16,9 17,0 17,1 17,2 17,3 17,4 17,5 17,6 17,8 17,9 18,0 18,1 18,2 18,3 | -0,4 0,2 0 0,2 0,4 0,6 0,5 0,4 0,3 0,2 0,1 0 0,2 0,4 | ||||
| 2004 2005 | 17,9 18,0 | 18,4 18,5 | -0,5 0,5 | ||||
| Итого | 283,7 | 283,2 | 4,9 | ||||
Рассчитаем нулевое среднее.
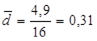
Нулевое среднее относительно приближено к нулю, значит, выбранная линия не содержит систематической ошибки, модель адекватна.
 2020-01-14
2020-01-14 103
103