Наиболее применяемыми числовыми характеристиками совокупности значений случайной величины являются:
– среднее значение, характеризующее центр группирования случайной величины;
– среднеквадратическое отклонение и коэффициент вариации, являющиеся характеристиками рассеивания случайной величины.
Так как 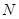 > 25, то характеристики вычисляются по зависимостям:
> 25, то характеристики вычисляются по зависимостям:
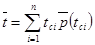 , (7)
, (7)
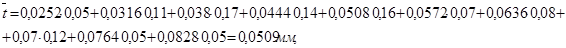
 , (8)
, (8)
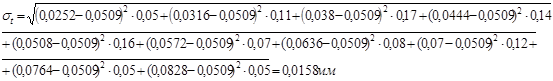
Анализ зависимостей для определения 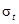 показывает, что его значение зависит не только от величины рассеивания, но и от абсолютных значений СВ. От этого недостатка свободен коэффициент вариации
показывает, что его значение зависит не только от величины рассеивания, но и от абсолютных значений СВ. От этого недостатка свободен коэффициент вариации  , определяемый по зависимости:
, определяемый по зависимости:
 (9)
(9)
где при N > 25 t см= t н1 –0,5 h;
t см= t н1 –0,5 h =0,022 - 0,5∙0,0064= 0,0188 мм.
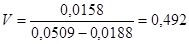
Проверка однородности информации об износах
Проверку на выпадающие точки проводят по критерию Ирвина  , который вычисляют по зависимости:
, который вычисляют по зависимости:
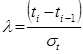 , (10)
, (10)
где 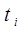 и
и 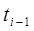 – смежные значения случайной величины вариационного ряда.
– смежные значения случайной величины вариационного ряда.
Проверку начинают с крайних значений случайной величины. Вычисленное 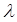 сравнивают с табличным значением
сравнивают с табличным значением  ,
,  взятом из табл. В.1 [1], при доверительной вероятности
взятом из табл. В.1 [1], при доверительной вероятности 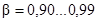 и числе наблюдений
и числе наблюдений  .
.
При  переходят к проверке однородности следующего значения СВ. При
переходят к проверке однородности следующего значения СВ. При  проверяемое значение СВ признают выпадающим (экстремальным), и оно исключается из выборочной совокупности наблюдений.
проверяемое значение СВ признают выпадающим (экстремальным), и оно исключается из выборочной совокупности наблюдений.
Пример решения:
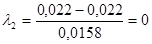 .
.
 при N=100, значение критерия Ирвина
при N=100, значение критерия Ирвина 
Вычисленные значения критерия Ирвина запишем в таблицу 5.
Таблица 5 – Значения критерия Ирвина
| - | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0,063 | 0,126 | 0,063 |
| 0 | 0 | 0,126 | 0,063 | 0,063 | 0 | 0 | 0 | 0 | 0,126 |
| 0,126 | 0 | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0,063 | 0 |
| 0,126 | 0 | 0,063 | 0,063 | 0,063 | 0 | 0,189 | 0,063 | 0 | 0,126 |
| 0,126 | 0,063 | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0 | 0 |
| 0,063 | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0 | 0 | 0,189 |
| 0,063 | 0,063 | 0 | 0 | 0 | 0 | 0,063 | 0,063 | 0 | 0,063 |
| 0,063 | 0 | 0 | 0,063 | 0,063 | 0,063 | 0 | 0,063 | 0,063 | 0,253 |
| 0,126 | 0 | 0 | 0 | 0 | 0 | 0,063 | 0,063 | 0,126 | 0 |
| 0 | 0,063 | 0,063 | 0 | 0,063 | 0,063 | 0 | 0 | 0 | 0 |
Вычисленные значения  сравним с табличным значением
сравним с табличным значением 
Взятом из таблицы В.1 [1] при доверительной вероятности  и числе наблюдений N=100
и числе наблюдений N=100
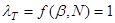
Отсюда следует, что все точки однородны.
 2020-01-14
2020-01-14 109
109








