2020-01-14
157
Схема внутреннего контура оптимальной САР представлена на рисунке 3.
Внутренний контур оптимальной САР
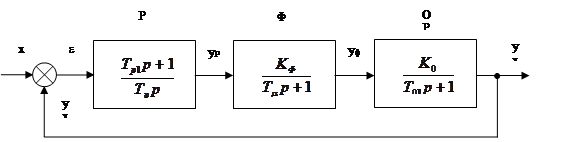
Рис.3
Определим передаточные функции разомкнутой и замкнутой оптимальных систем.
Wраз1 (p) - оптимальная по техническому оптимуму.
Расчет графиков оптимальных САР аналитическим способом
Применив обратное преобразование Лапласа, можно получить следующее выражение для переходной функции замкнутого контура.
Характеристическое уравнение для данного случая
Задаваясь временем t и пользуясь выражением (3) составляем таблицу 1, а затем строим кривую переходного процесса (рис 4).
Расчет данных для построения кривой переходного процесса
Таблица 1
Кривая переходного процесса h (t) замкнутой САР
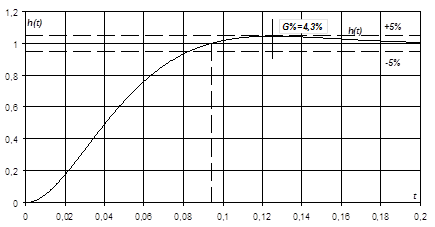
Рис.4
2.5 Исследование динамических свойств внутреннего контура регулирования САР при изменении постоянной времени регулятора Tр.
Будем исследовать САР для трех случаев;
при 
c
Передаточные функции разомкнутых и замкнутых САР
Из выражения 1 получим передаточные функции разомкнутых и замкнутых САР для различных Tр.
Для первого случая:
Разомкнутая САР представляет собой последовательно соединенные интегральное и апериодическое звено.
где T = 
=0,028с, а 
=0,707.
Замкнутая САР - колебательное звено с оптимальным коэффициентом затухания.
Для второго случая (аналогично первому):
где T = 
=0,02с, а 
=0,5.
Для третьего случая:
где T = 
=0,04с, а 
.
Построение ЛАЧХ и ЛФЧХ замкнутой и разомкнутой САР
Задаваясь значениями частоты строим ЛАЧХ и ЛФЧХ используя выражения выведенные в п.2.5.1.
Построение асимптотических ЛАЧХ и ЛФЧХ для разомкнутой САР произведено на рис.5, а для замкнутой - на Рис.6.
Данные для построения ЛФЧХ приведены в таблице 2.
Таблица 2. Расчетные данные для построения ЛФЧХ замкнутых и разомкнутых САР.
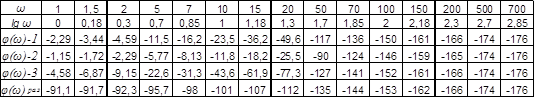
Логарифмические частотные характеристики разомкнутой САР
Рис.5. Логарифмические частотные характеристики замкнутой САР
Рис.6
