Всі експериментальні дослідження в техніці базуються на вимірах. Задача зводиться до встановлення мінімального, але достатнього об’єму вибірки (числа вимірювань) Nmin при заданих значеннях надійного інтервалу 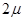 і надійної ймовірності. При виконанні вимірювання необхідно знати їх точність Δ, яку характеризують δ0 – середньоарифметичне значення середньоквадратичного відхилення
і надійної ймовірності. При виконанні вимірювання необхідно знати їх точність Δ, яку характеризують δ0 – середньоарифметичне значення середньоквадратичного відхилення 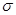 :
:
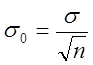 ;
; 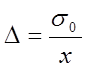 (6.25)
(6.25)
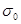 - середня помилка.
- середня помилка.
Надійний інтервал помилки вимірювання Δ визначається аналогічно, як і для вимірювань 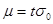 . За допомогою t легко визначити надійну ймовірність помилки вимірювання з таблиці 6.1.
. За допомогою t легко визначити надійну ймовірність помилки вимірювання з таблиці 6.1.
В дослідженнях за заданою точністю Δ і надійною ймовірністю визначають мінімальну кількість вимірювань, яка гарантує потрібні значення Δ і Ф(t).
Аналогічно рівнянню (6.23) з урахуванням (6.25) запишемо
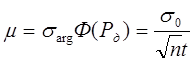 (6.26)
(6.26)
звідси, приймаючи  Nmin=n, будемо мати
Nmin=n, будемо мати

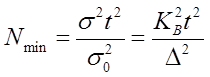 (6.27)
(6.27)
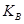 - коефіцієнт варіації (мінливості), %;
- коефіцієнт варіації (мінливості), %;
D - точність вимірювання, %.
Для визначення 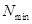 можна прийняти таку послідовність:
можна прийняти таку послідовність:
1. Нехай n – кількість вимірів від 20 до 50, в залежності від складності дослідів.
2. Визначають середнє квадратичне відхилення m (6.21).
3. Встановлюють необхідну точність вимірювань m, D, яка повинна бути не менше точності приладу.
4. Установлюють нормативне відхилення t, значення якого задають, наприклад при великій точності вимірювань t=3.0, при малій – t=2.0, можна прийняти t=2.5.
5. Із (6.26) визначають 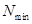 . В процесі експерименту число вимірів не повинно бути менше
. В процесі експерименту число вимірів не повинно бути менше 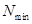 .
.
Приклад
при прийманні споруди, комісія в якості одного із параметрів, вимірює її ширину. Необхідно виконати 25 вимірів, допустиме відхилення параметра 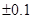 м. Необхідно визначити, з якою вірогідністю комісія оцінює даний параметр. Попереднє обчислення значення
м. Необхідно визначити, з якою вірогідністю комісія оцінює даний параметр. Попереднє обчислення значення 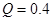 м.
м.
Допустиме відхилення параметра 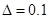 м. з рівняння (6.27) запишемо
м. з рівняння (6.27) запишемо 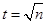 .
. 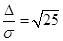 ;
; 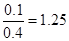 . У відповідності з таблицею (6.). Надійна ймовірність для
. У відповідності з таблицею (6.). Надійна ймовірність для 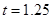
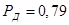 це низька ймовірність. Похибка перевищує надійний інтервал
це низька ймовірність. Похибка перевищує надійний інтервал 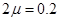 м, згідно формули (6.),буде зустрічатися один раз із
м, згідно формули (6.),буде зустрічатися один раз із 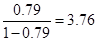 , тобто із чотирьох вимірювань. Це не допустимо. Вирахуємо мінімальну кількість вимірів, з надійною ймовірністю РД , рівною 0,9 і 0,95. За формулою (6.27) маємо
, тобто із чотирьох вимірювань. Це не допустимо. Вирахуємо мінімальну кількість вимірів, з надійною ймовірністю РД , рівною 0,9 і 0,95. За формулою (6.27) маємо 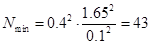 виміри при РД =0,90 і 64 виміри при РД =0,95. Результати вимірювань за допомогою
виміри при РД =0,90 і 64 виміри при РД =0,95. Результати вимірювань за допомогою 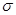 і
і 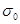 справедливі при
справедливі при 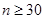 . Для знаходження границь надійного інтервалу при малих значеннях застосовують метод запропонований в 1908 році англійським математиком
. Для знаходження границь надійного інтервалу при малих значеннях застосовують метод запропонований в 1908 році англійським математиком
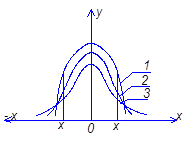
В.С. Гессетом (псевдонім Стьюдент). Криві розподілення Стьюдента у разі 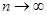 переходять в криві нормального розпреділення (рис. 6.1).
переходять в криві нормального розпреділення (рис. 6.1).
Для малої вибірки надійний інтервал
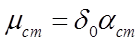 (6.28)
(6.28)
де 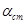 - коефіцієнт Стьюдента, який приймається з табл. 6.2 в залежності від значення надійної ймовірності Фст знаючи mст, можна визначити дійсне значення величини, що вивчається для малої вибірки:
- коефіцієнт Стьюдента, який приймається з табл. 6.2 в залежності від значення надійної ймовірності Фст знаючи mст, можна визначити дійсне значення величини, що вивчається для малої вибірки:
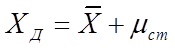 (6.29).
(6.29).
Можлива інша постановка задачі. Маючи n відомих вимірів малої вибірки необхідно визначити необхідну ймовірність РД за умовою, що похибка середнього значення не вийде за межі 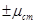 .
.
Задачу розв’язують у такій послідовності:
1. Визначають середнє значення 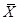 ,
, 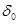 і
і 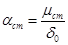 .
.
2. За допомогою величини 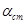 , відомого n і таблиці 6.2 визначають надійну ймовірність.
, відомого n і таблиці 6.2 визначають надійну ймовірність.
 2020-04-20
2020-04-20 111
111








