2020-04-20
530
Число, навколо якого групуються значення випадкової величини, є характеристикою положення; число, що характеризує ступінь розкиданості значень випадкової величини навколо характеристики положення, є характеристикою розсіяння.
Однією з основних характеристик положення випадкових величин є математичне сподівання.
Математичним сподівання випадкової дискретної величини називається сума добутків окремих значень, що їх набуває на їх, відповідні ймовірності.
Нехай дано ряд розподілу дискретної випадкової величини:
Таблиця 6.1.
| Х | Х1 | Х2 | ..... | Хп |
| Р | Р1 | Р2 | ..... | Рп |
Позначивши математичне сподівання через Е(х) за означенням, дістанемо:
(6.7)
Математичне сподівання часто називають центром розподілу або центром розсіяння. Математичне сподівання випадкової величини дорівнює середній їй, значень зваженій за ймовірностями:
ПРИКЛАД.
Дано розподіл кількості написаних знаків за 5 хв. певною групою студентів (табл.6.2).Визначити математичне сподівання (середню кількість знаків, що їх може написати студент за 5 хв.) кількості написаних знаків:
|
|
|
Таблиця 6.2
| Кількість написаних знаків за 5 хв. | 230 | 254 | 262 | 274 | 281 | 282 | 285 | 302 | 307 | 308 |
| Імовірність Рі | 0,075 | 0,125 | 0,025 | 0,075 | 0,175 | 0,25 | 0,025 | 0,10 | 0,10 | 0,05 |
| Хі * Рі | 17,25 | 31,75 | 6,55 | 20,55 | 49,175 | 70,50 | 7,125 | 30,2 | 30,7 | 15,40 |
РОЗВ’ЯЗАННЯ
Математичне сподівання визначається за формулою 6.7.
Отже, в середньому один студент за 5 хв. напише 279 знаків.
Математичне сподівання неперервної випадкової величини визначається за формулою:
(6.8)
де f(x)--функція щільності розподілу iмовірностей.
Властивості математичного сподівання:
Ø Математичне сподівання сталої величини дорівнює цій самій сталій:
E(a) = a (6.9)
Ø Сталий множник можна виносити за знак математичного сподівання:
E(cX) = cE(X) (6.10)
Ø Математичне сподівання алгебраїчної суми випадкових величин дорівнює алгебраїчній сумі їх математичних сподівань:
E(X±Y±Z±…±W)=E(X)±E(Y)±E(Z)±…±E(W) (6.11)
Ø Математичне сподівання добутку незалежних випадкових величин дорівнює добутку їх математичних сподівань:
E(XY)=E(X)*E(Y) (6.12)
Ø Математичне сподівання випадкової величини завжди обмежене найбільшим і найменшим її значеннями:
xmin < E(X) < xmax (6.13)
6.3 Дисперсія
Другою важливою характеристикою випадкової величини є дисперсія, яка характеризує ступінь розсіяння значень випадкової величини навколо її середньої. Математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання називається дисперсією і позначається через D(x) або σ2.
|
|
|
Для дисперсії випадкової величини дисперсія обчислюється за формулою:
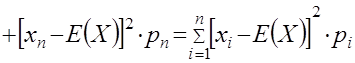(6.14)
Дисперсія має такі основні властивості:
Ø Дисперсія сталої величини дорівнює нулю. Справді, нехай X=c. Тоді:
D(X)=D(c)=E(c-c)2=E(c-c)2=0 (6.15)
через те що середнє значення сталої величини дорівнює самій сталій.
Ø Сталий множник можна винести за знак дисперсії. При цьому його треба піднести до квадрата:
(6.16)
Ø Дисперсія суми кількох незалежних випадкових величин дорівнює сумі їх, дисперсій:
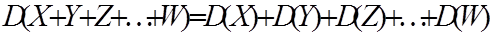(6.17)
Ø Дисперсія випадкової величини дорівнює середньому значенню її квадрата мінус квадрат її середнього значення:
(6.18)
Величина
(6.19)
називається середнім квадратичним відхиленням і є мірою для характеристики ступеня розсіяння випадкової величини.
ПРИКЛАД
За даними прикладу попереднього параграфа (табл.6.2) обчислити дисперсію та середнє квадратичне відхилення.
РОЗВ’ЯЗАННЯ
Дисперсію обчислюємо за формулою (6.14):
σ2=(230-279)2·0,075+ (254-279)2·0,125+ (262-279)2·0,25+ (274- -279)2·0,075+ (281-279)2·0,175+ (282-279)2·0,25+ (285-279)2·0,025+ +(302-279)2·0,1+ (307-279)2·0,1+ (308-279)2·0,05=444
Середнє квадратичне відхилення обчислюємо за формулою (6.19):
За міру розсіяння можна взяти модуль імовірностей, який визначається за формулою:
(6.20)
Інколи розсіяння нормальної кривої характеризують мірою точності, яка є оберненою величиною до модуля ймовірностей:
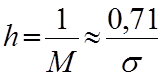(6.21)
Для великої вибірки і нормального закону розподілу загальною оціночною характеристикою вимірювання є дисперсія й коефіцієнт варіації.
, 
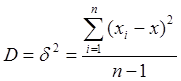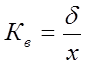(6.22)
Дисперсія характеризує однорідність вимірювання. Чим вище Д, тим більший розкид вимірів. Коефіцієнт варіації характеризує мінливість. Чим вище Кв, тим більша мінливість вимірювань відносно середніх значень. Кв оцінює також розкид при оцінюванні декількох вибірок.
В цій задачі можливий другий варіант. На основі визначених даних встановлена певна (надійна) ймовірність Рд. Дуже часто її приймають рівною 0,9; 0,95; 0,9973. Необхідно встановити точність вимірювання, тобто надійний інтервал 2µ.
Так як 
, то по таблиці можна визначити половину надійного інтервалу:
(6.23),
де Ф(Рд) – аргумент функції Лапласа, або при n<10 Стьюдента (табл. 6.2). Надійний інтервал характеризує точність вимірювання даної вибірки, а надійна ймовірність – вірогідність вимірювання.
Приклад.
Виконано 30 вимірювань міцності одежи ділянки автомобільної дороги. При цьому середній модуль пружності одежи Еэ=170 МПа. Визначене значення середньоквадратичного відхилення є 
=3.1 МПа. Визначити точність і вірогідність експерименту.
Точність вимірювання визначаємо для різних рівнів вірогідної ймовірності, прийнявши, відповідно значення argФ(t) із таблиці 6.1: Рд=0,9; 0,95; 0,9973; µ= 
;
µ=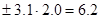 
;
µ= 
МПа.
Отже для даного засобу і методу надійний інтеграл зростає приблизно в два рази, якщо Рд збільшити тільки на 10%. Необхідно визначити вірогідність вимірів для встановленого надійного інтервалу, наприклад 
за формулою (6.5) 
.
За табл. 6.1 для 2.26 визначаємо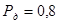 
. Це означає, що в заданий надійний інтервал із 100 вимірювань не попадає тільки три.
Значення 1 - Ф(t) називають рівнем значності. Із нього виходить, що при нормальному законі розподілу похибка, яка перевищує надійний інтервал, буде зустрічатися один раз із nи вимірів:
(6.24)
або вибірковувати одне із nи вимірів.
