2020-04-20
192
При вимірюванні один із результатів різко відрізняється від інших, виникає підозра, що допущена груба помилка.
Позначимо значення, яке відрізняється від ряду інших вимірів – статистичного ряду –Х*, а всі останні результати Х1, Х2..., Хn, підрахуємо середнє арифметичне: 
і порівняємо абсолютну величину різниці 
х* -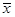 
звеличиною 
. Для отриманого відношення
підрахуємо ймовірність 1-2Ф(t) за допомогою таблиці I (додаток I). Може бути два випадки:
1). Якщо, відношення, що розглядається, буде мати значення не менше ніж t, при умові, що значення х* не має грубої помилки, що помилка результату х* є випадковою.
2).Якщо підрахована таким чином ймовірність буде дуже малою, то значення, яке “вискакує” має грубу помилку і його необхідно виключити з ряду. Яку ймовірність рахувати дуже малою, залежить від конкретних умов розв’язку задачі; якщо вибрати (призначити) дуже низький рівень малих ймовірностей, то грубі помилки можуть залишитися, якщо ж взяти цей рівень невизначено великим, то можна виключити результати із випадковими помилками, необхідними для правильної обробки результатів вимірювання. Взагалі приймають один з трьох рівнів малих ймовірностей:
Ø 5% рівень (виключаються помилки, ймовірність появи яких менше 0,05);
Ø 1% рівень (виключаються помилки, ймовірність появи яких менше 0,01);
Ø 0,1% рівень (виключаються помилки, ймовірність появи яких менше 0,001);
При вибраному рівні a малих ймовірностей, значення х*, яке “вискакує” має грубу помилку, якщо для відповідного відношення t ймовірність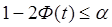 
, тоді підкреслюють, що х* має грубу помилку з надійністю висновку 
, значення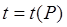 
, для якого 
, і, значить, 
, називається критичним значенням відношення t при надійності Р. Так, якщо 
(1% рівень), то Р=0,99, критичне значення 
(див. Додаток I), і як тільки відношення t перевищить це критичне значення, ми можемо бракувати (значення х*, яке “вискакує” з надійністю висновка 0,99). Підкреслимо, що цей спосіб застосовується тоді, коли величина d середньої квадратичної помилки точно відома раніше.
Найбільш простий спосіб вилучення із статистичного ряду х*, яке різко виділяється є правило трьох сігм. Розкид випадкових величин від середнього значення не перевищує
хmax,min= 
(6.38).
Більш вірогідний є метод, який базується на використанні надійного інтервалу. Нехай є статистичний ряд малої вибірки, який підчиняється закону нормального розподілу. При наявності грубих помилок критерій їх появи:
; 
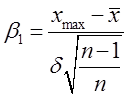; (6.39)
де хmax, xmin найбільше і найменше значення із n вимірів.
В таблиці 6.3 наведенні максимальні значення 
, які виникають внаслідок статистичного розкиду. Якщо 
, то значення 
необхідно виключити із статистичного ряду, як грубу помилку. При 
виключається величина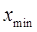 
. Після виключення грубих помилок визначають нові значення 
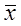і 
із 
або 
вимірів.
Таблиця 6.3
| n | bmax при Рд | n | bmax при Рд | |||||
| 0.90 | 0.95 | 0.99 |  0.90
| 0.95 | 0.99 | |||
| 3 4 5 6 7 8 9 10 11 12 13 14 | 1.41 1.64 1.79 1.89 1.97 2.04 2.10 2.15 2.19 2.23 2.26 2.30 | 1.41 1.69 1.87 2.00 2.09 2.17 2.24 2.29 2.34 2.39 2.43 2.46 | 1.41 1.72 1.96 2.13 2.26 2.37 2.46 2.54 2.61 2.66 2.71 2.76 | 15 16 17 18 19 20 25 30 35 40 45 50 | 2.33 2.35 2.38 2.40 2.43 2.45 2.54 2.61 2.67 2.72 2.76 2.8 | 2.49 2.52 2.55 2.58 2.60 2.62 2.72 2.79 2.85 2.90 2.95 2.99 | 2.80 2.84 2.87 2.90 2.93 2.96 3.07 3.16 3.22 3.28 3.33 3.37 | |
Третій спосіб: задається надійна ймовірність РД із таблиці 6.4 в залежності від 
знаходять коефіцієнт q. Визначають гранично допустиму абсолютну похибку окремого виміру
(6.40).
Якщо 
, то 
виключається. Визначають відносну похибку результатів серії вимірювань при заданій надійній ймовірності РД;
(6.41)
- коефіцієнт Стьюдента.
Якщо похибка серії вимірювань сумісна з похибкою приладу Впр, то границі надійного інтегралу
(6.42)
Таблиця 6.4
| Значення q при РД | ||||
| n | 0.95 | 0.98 | 0.99 | 0.995 |
| 2 3 4 5 6 7 8 9 10 12 14 16 18 20 | 4.97 3.56 3.04 2.78 2.62 2.51 2.43 2.37 2.29 2.24 2.20 2.17 2.15 | 38.97 8.04 5.08 4.10 3.64 3.36 3.18 3.05 2.96 2.83 2.14 2.68 2.64 2.60 | 77.96 11.46 6.53 5.04 4.36 3.96 3.71 3.54 3.41 3.23 3.12 3.04 3.00 2.93 | 779.7 36.5 14.46 9.43 7.41 6.37 5.73 5.31 5.01 4.62 4.37 4.20 4.07 3.93 |
Формулою (6.35) слід користуватися при 
. Якщо ж 
, то надійний інтервал визначають за допомогою формул (6.31).
Приклад
Для визначення якості знань студентів з даної дисципліни, дають контрольні роботи 120 студентам. Імовірність виконання контрольної роботи на “відмінно” становить 0,3. яка імовірність того, що контрольні роботи напишуть на відмінно:
а)Не менше як 25 і не більше як 46 студентів;
б)Не менше як 50?
Розв’язання.
Дано:
а) p=0,3; m1=25; m2=46; n=120.
б) p=0,3; m1=50; m2=120; n=120.
а) x1=m1-np=25-120*0,3=25-36= -9
x2=m2-np=46-120*0,3=46-36=10
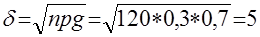
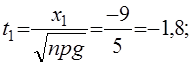
б) x1=m1-np=50-120*0,3=50-36= 14
x2=m2-np=120-120*0,3=120-36=84
Тобто, майже неможливо, щоб більше 50 студентів написали контрольну роботу на “відмінно” за даних умов.
