Структурный и кинематический анализ главного механизма
Выходные данные согласно заданию к курсовому проекту.
1. Схема двухпоршневого V - образного насоса (рис. 1.1)
2. Угловая скорость кривошипа  , с-1 16
, с-1 16
3. Погонная единица массы 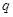 , кг/м 19
, кг/м 19
4. Коэффициент  (
( ) 6,2
) 6,2
5. Коэффициент  (
( ), Н/м 5000
), Н/м 5000
6. Угол 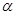 100
100
7. Длина кривошипа 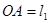 , мм 140
, мм 140
8. Длина шатуна  , мм 560
, мм 560
9. Неравномерность хода  1/5
1/5

Рис. 1.1. Кинематическая схема механизма
Структурный анализ механизма
Механизм двухпоршневого горизонтального насоса состоит из 6 звеньев:
1 – кривошип ОА;
2, 3 – шатуны АB и AE;
4, 5 – ползуны (поршни) B и E;
6 – стойка.
Звенья механизма образуют 7 кинематических пар, из которых 5 вращательных и 2 поступательные.
Согласно формуле Чебышева степень свободы определиться как

где  - количество звеньев,
- количество звеньев, 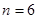 ;
;
 - количество кинематических пар
- количество кинематических пар  класса,
класса,  ;
;
 - количество пар
- количество пар  класса,
класса,  .
.
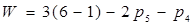
Таким образом, механизм имеет одну степень свободы.
На рис. 1 изображена структурная схема механизма с разбиением на группы Асура и начальный механизм.
Структурная схема наглядно показывает, что механизм состоит из начального механизма 1 класса (стойка 6 и кривошип 1) и двух групп Асура (шатун 2 и ползун 4, шатун 3 и ползун 5).

Рис. 1.2 Структурная схема механизма
Структурная формула механизма:

Механизм относится к механизмам II класса по классификации И. И. Артоболевского.
Построение плана положений механизма
На листе формата А1 изображаем в масштабе план положений механизма. План строим в такой последовательности. Выбираем масштаб построения:

Выбираем произвольную точку О и из нее описываем окружность радиуса ОА. Начальное положение точки А (АО) выбираем согласно исходной схемы на продолжении направляющей ОE, при пересечении ее с вычерченной окружностью. От точки АО в направлении вращения кривошипа ОА разбиваем окружность на 12 равных частей, через каждые 30 градусов, проставляя при этом последовательно точки А1, А2 и т. д. Соединив полученные точки с центром окружности О, получим 12 положений кривошипа ОА. Точка E принадлежит шатуну АE и ползуну E и движется поступательно по направляющей ОE, поэтому для построения плана положений звена АE из каждой точки А раствором циркуля, равным длине шатуна АE в принятом масштабе, делаем засечки на направляющей, получая точки E1, E2 и т. д. План положений для звена AB строим аналогично.
Построение планов скоростей
Паны скоростей строятся по векторным уравнениям, которые составляются отдельно для каждой группы Асура в порядке присоединения их к ведущему звену.
Для ведущего звена ОА определяем величину скорости точки А:

Вектор 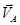 перпендикулярен радиусу, т. е. отрезку ОА, и направлен в сторону, определяемую направлением
перпендикулярен радиусу, т. е. отрезку ОА, и направлен в сторону, определяемую направлением  . Задаемся масштабом плана скоростей
. Задаемся масштабом плана скоростей
 ,
,
и вычисляем отрезок 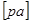 , изображающий в выбранном масштабе вектор
, изображающий в выбранном масштабе вектор 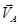


Из произвольной точки Р, называемой полюсом плана скоростей, откладываем в указанном направлении отрезок 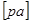 длиной 44,8 мм.
длиной 44,8 мм.
Составляем векторное уравнение, по которому определим скорость точки B, принадлежащей шатуну АB и ползуну B.
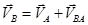
Скорость точки А известна, скорость относительного вращения точки B вокруг точки А перпендикулярна радиусу вращения отрезку АB и определяется по формуле
 .
.
Скорость точки B направлена вдоль направляющей АB. Таким образом, получаем векторное уравнение, в котором два вектора известны по направлению, но неизвестны по величине, а третий вектор известен по направлению и по величине. Решая это векторное уравнение графическим способом, получим план скоростей для группы Асура, состоящей из звеньев 2 и 4. В соответствии с векторным уравнением через конец вектора 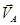 (точку а) проводи направление вектора
(точку а) проводи направление вектора  , перпендикулярное BА, а через полюс
, перпендикулярное BА, а через полюс  - направление вектора
- направление вектора 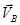 , параллельное АB. На пересечении этих направлений поставим точку B, а отрезки
, параллельное АB. На пересечении этих направлений поставим точку B, а отрезки 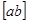 и
и  в масштабе будут представлять скорости
в масштабе будут представлять скорости  и
и 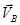 . Для определения их величины достаточно измерить соответствующие отрезки и умножить их на масштабный коэффициент
. Для определения их величины достаточно измерить соответствующие отрезки и умножить их на масштабный коэффициент 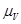 :
:


Пользуясь построенным планом скоростей, можно определить угловую скорость  по формуле:
по формуле:

Для определения направления  переносим вектор
переносим вектор 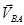 в точку B механизма и рассматриваем движение этой точки относительно точки А по направлению скорости
в точку B механизма и рассматриваем движение этой точки относительно точки А по направлению скорости  .
.
Аналогично строим план скоростей для группы Ассура (звенья 3 и 5) по уравнению:
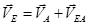
и определяем угловую скорость шатуна AE:

Для определения направления 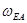 переносим вектор
переносим вектор  в точку E и рассматриваем движение этой точки относительно точки A.
в точку E и рассматриваем движение этой точки относительно точки A.
Изложенным выше способом строим планы скоростей для остальных 11 положений.
Результаты построения заносим в таблицу 1.1.
Таблица 1.1
| Полож. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| , град | 0 | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 | 330 |
| [PA], мм | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 | 44,80 |
| [AВ], мм | 8,03 | 29,34 | 42,25 | 44,16 | 34,77 | 15,76 | 8,03 | 29,34 | 42,25 | 44,16 | 34,77 | 15,76 |
| [РВ], мм | 46,10 | 39,94 | 18,94 | 9,70 | 34,38 | 45,80 | 42,14 | 28,70 | 11,71 | 5,86 | 23,21 | 38,40 |
| [AЕ], мм | 44,80 | 39,10 | 22,94 | 0,00 | 22,94 | 39,10 | 44,80 | 39,10 | 22,34 | 0,00 | 22,94 | 39,10 |
| [РЕ], мм | 0,00 | 17,51 | 33,83 | 44,80 | 43,77 | 27,29 | 0,00 | 27,29 | 43,77 | 44,80 | 33,83 | 17,51 |
| VAВ, м/с | 0,40 | 1,47 | 2,11 | 2,21 | 1,74 | 0,79 | 0,40 | 1,47 | 2,11 | 2,21 | 1,74 | 0,79 |
| VВ, м/с | 2,30 | 2,00 | 0,95 | 0,48 | 1,72 | 2,29 | 2,11 | 1,43 | 0,59 | 0,29 | 1,16 | 1,92 |
| VAЕ, м/с | 2,24 | 1,96 | 1,15 | 0,00 | 1,15 | 1,96 | 2,24 | 1,96 | 1,12 | 0,00 | 1,15 | 1,96 |
| VЕ, м/с | 0,00 | 0,88 | 1,69 | 2,24 | 2,19 | 1,36 | 0,00 | 1,36 | 2,19 | 2,24 | 1,69 | 0,88 |
| ВА, с-1 | 0,72 | 2,62 | 3,77 | 3,94 | 3,10 | 1,41 | 0,72 | 2,62 | 3,77 | 3,94 | 3,10 | 1,41 |
| ЕА, с-2 | 4,00 | 3,49 | 2,05 | 0,00 | 2,05 | 3,49 | 4,00 | 3,49 | 2,00 | 0,00 | 2,05 | 3,49 |
Построение планов ускорений
Определяем ускорение точки А. Так как кривошип по условию движется равномерно (угловое ускорение равно нулю), то ускорение точки А состоит только из нормальной составляющей, которая равна:

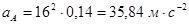
Вектор  направлен по радиусу к центру – от точки А к точке О. Задаемся масштабом плана ускорений
направлен по радиусу к центру – от точки А к точке О. Задаемся масштабом плана ускорений  и вычисляем длину отрезка
и вычисляем длину отрезка 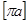 , изображающего в масштабе вектор
, изображающего в масштабе вектор 
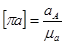

Из произвольной точки  , называемой полюсом плана ускорений, в направлении вектора
, называемой полюсом плана ускорений, в направлении вектора  откладываем отрезок
откладываем отрезок  .
.
Переходим к группе Ассура (звенья 2, 4).
Векторное ускорение для точки С группы имеет вид

Ускорение  слагается из нормальной и касательной составляющих
слагается из нормальной и касательной составляющих

Ускорение  по величине равно
по величине равно
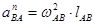
Вычисляем его величину и откладываем в масштабе от точки а плана ускорений в направлении от точки B к точке А механизма отрезок  , равный по величине:
, равный по величине:
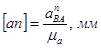
Ускорение 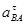 определяется по формуле:
определяется по формуле:

Вектор  направлен вдоль направляющей ОB. Таким образом, получаем в векторном уравнении два неизвестных по величине, но известных по направлению вектора. Для их определения продолжим построение плана ускорений. Из точки
направлен вдоль направляющей ОB. Таким образом, получаем в векторном уравнении два неизвестных по величине, но известных по направлению вектора. Для их определения продолжим построение плана ускорений. Из точки  плана проведем направление вектора
плана проведем направление вектора 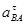 перпендикулярно BА, а из точки
перпендикулярно BА, а из точки  - параллельно направлению
- параллельно направлению  (параллельно направляющей ОB). На пересечении этих направлений поставим точку b. Получаем отрезки
(параллельно направляющей ОB). На пересечении этих направлений поставим точку b. Получаем отрезки  и
и  , которые в масштабе изображают соответственно ускорение
, которые в масштабе изображают соответственно ускорение  и
и 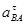 , т. е.
, т. е.
 и
и 
Зная 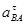 , определяем величину углового ускорения
, определяем величину углового ускорения  :
:

Направление углового ускорения определится после переноса вектора 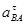 в точку B механизма.
в точку B механизма.
Для группы Ассура (звенья 3, 5) построение выполняется аналогично по векторному уравнению:
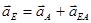
Строим план ускорений для положения 2.
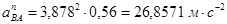
Строим план ускорений для положения 7.
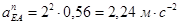
Результаты построения заносим в таблицу 1.2
Таблица 1.2
| Пол. | 
| 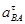
| 
| 
| 
| 
| 
| 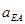
| 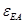
| 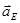
|
| м×с-2 | м×с-2 | м×с-2 | с-2 | м×с-2 | м×с-2 | м×с-2 | м×с-2 | с-2 | м×с-2 | |
| 2 | 25,41 | 10,12 | 27,31 | 18,08 | 58,14 | 2,35 | 31,27 | 31,36 | 55,84 | 22,4 |
| 7 | 12,25 | 25,58 | 28,31 | 45,68 | 15,41 | 6,83 | 17,48 | 18,77 | 31,22 | 35,63 |
Кинематические диаграммы
Диаграммы строятся для 12 положений механизма, которые были изображены на плане положений. Полный оборот кривошипа ОА соответствует одному кинематическому циклу
Рассмотрим построение диаграммы перемещения ползуна В 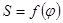 . Проводим координатные оси
. Проводим координатные оси  и
и 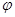 . На оси
. На оси 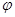 откладываем 12 равновеликих отрезков 0-1, 1-2 и т. д., соответствующих углу поворота кривошипа на 1/12 часть оборота (300). Через точки 1, 2, 3 и т. д. проводим ординаты и откладываем на них отрезки, равные координатам токи с -
откладываем 12 равновеликих отрезков 0-1, 1-2 и т. д., соответствующих углу поворота кривошипа на 1/12 часть оборота (300). Через точки 1, 2, 3 и т. д. проводим ординаты и откладываем на них отрезки, равные координатам токи с -  в соответствующих положениях, отсчитываемых от крайнего нижнего положения точки В. Соединяя полученные точки плавной кривой линией, изображаем диаграмму
в соответствующих положениях, отсчитываемых от крайнего нижнего положения точки В. Соединяя полученные точки плавной кривой линией, изображаем диаграмму  .
.
При равномерном вращении кривошипа угол его поворота  пропорционален времени. Поэтому полученная диаграмма
пропорционален времени. Поэтому полученная диаграмма 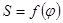 является одновременно диаграммой зависимости перемещения ползуна от времени
является одновременно диаграммой зависимости перемещения ползуна от времени  . Разница будет лишь в масштабах абсцисс.
. Разница будет лишь в масштабах абсцисс.
Масштаб перемещения 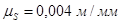 . Масштаб углов
. Масштаб углов  равен
равен

где  - отрезок (мм) по оси
- отрезок (мм) по оси 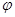 , изображающий полный оборот кривошипа ОА (2p).
, изображающий полный оборот кривошипа ОА (2p).
Масштаб оси времени 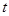 диаграммы равен
диаграммы равен
 ,
,
где Т – период одного оборота кривошипа, который определяется по формуле:

Таким образом, для получения масштаба времени 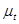 достаточно разделить масштаб угла поворота
достаточно разделить масштаб угла поворота 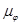 на величину угловой скорости кривошипа
на величину угловой скорости кривошипа 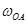 .
.

Построение кривых  и
и 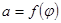 выполняется способом графического дифференцирования (методом хорд). При этом масштабные коэффициенты диаграмм определяются по формулам:
выполняется способом графического дифференцирования (методом хорд). При этом масштабные коэффициенты диаграмм определяются по формулам:
 ;
;
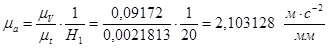
где Н и Н1 – полюсные расстояния диаграмм соответственно, мм.
Далее стоит построить диаграмму угловых перемещений шатунов АС и BD. Угловое перемещение измеряют в градусах, отсчитывая его от направляющих ОЕ и ОВ.
Поворот против часовой стрелки, относительно оси направляющих ползунов принимаем за положительный. Масштабный коэффициент  определится по формуле:
определится по формуле:
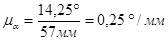 или
или 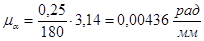
Выполнив графическое дифференцирование диаграммы углового перемещения, получим диаграмму угловой скорости. Масштабный коэффициент для данной диаграммы
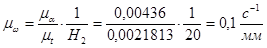
 2020-04-20
2020-04-20 125
125







