| И 2.33 | Определение. Двухполюсники эквивалентны, если их вольт-амперные характеристики совпадают. |
| И 2.34 | Частный случай. Два линейных пассивных двухполюсника эквивалентны, если их входные сопротивления (или проводимости) равны. |
Обоснование частного случая. В частном случае, когда двухполюсники являются линейными пассивными, определение эквивалентности (И 2.33) несколько упрощается. Действительно, если линейные пассивные двухполюсники имеют одинаковые входные сопротивления, то их вольт-амперные характеристики представляют собой прямые, проходящие через начало координат под одинаковыми углами к оси токов (рис. 2.9). Эти прямые совпадают, и, значит, требование определения И 2.33 выполняется.
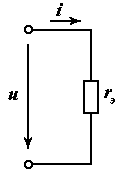
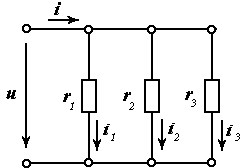
Пример 1. Эквивалентное сопротивление двухполюсника, содержащего несколько параллельно включенных резисторов. Сформулируем условие эквивалентности двух пассивных двухполюсников, показанных на рис. 2.14.
| 
|
Рис. 2.14. Эквивалентное преобразование параллельно включенных резисторов
Входная проводимость первого двухполюсника
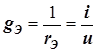 ,
,
входная проводимость второго
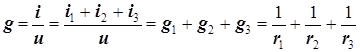 .
.
Двухполюсники эквивалентны, если 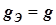 ; в таком случае
; в таком случае
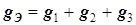 ,
,
или
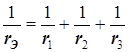 .
.
Любую из двух последних формул можно применить для эквивалентного преобразования трех параллельно включенных резисторов в один эквивалентный резистор. Эти формулы легко обобщаются на случай, когда несколько резисторов включены параллельно.
Пример 2. Эквивалентность источника напряжения и источника тока. Внешние характеристики источника напряжения (рис. 2.11) и источника тока (рис. 2.13) изображаются однотипными прямыми. Эти прямые совпадают, если у обоих источников одинаковы напряжения холостого хода и токи короткого замыкания:
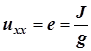 ,
, 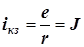 .
.
Эти формулы можно использовать для преобразования источника тока в эквивалентный источник напряжения (определить 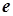 и
и 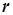 в схеме на рис. 2.10 по заданным
в схеме на рис. 2.10 по заданным 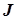 и
и 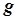 на схеме рис. 2.12) или обратного преобразования источника напряжения в эквивалентный источник тока (определить
на схеме рис. 2.12) или обратного преобразования источника напряжения в эквивалентный источник тока (определить 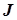 и
и 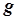 по заданным
по заданным 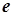 и
и 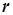 ).
).
 2020-04-07
2020-04-07 276
276








