Непрерывные случайные величины. Функция распределения вероятностей. Плотность вероятностей

 

Определение 1. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Определение 2. Функцией распределения вероятностей случайной величины 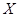  называют функцию , определяющую для каждого значения 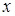 вероятность того, что случайная величина  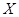примет значение меньшее 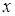, то есть

.

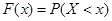Понятие функции распределения вводится как для непрерывной случайной величины, так и для дискретной случайной величины.

 

Часто вместо термина «функция распределения» используют термин «интегральная функция распределения».

Свойства функции распределения:

1. Значения функции распределения принадлежат отрезку :

.

2. Функция распределения есть неубывающая функция, то есть если 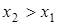, то

.

3. Вероятность того, что случайная величина примет значение, заключенное в промежутке

, равна приращению функции распределения на этом промежутке:

.

4. Вероятность того, что непрерывная случайная величина  примет одно определенное

значение 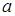, равна нулю:

.

5. Если возможные значения случайной величины принадлежат интервалу , то

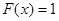 при ;

 при .

6. Если возможные значения непрерывной случайной величины расположены на всей оси

, то справедливы следующие предельные соотношения:

.

Для непрерывной случайной величины вводится понятие плотности распределения вероятностей.

Определение 3. Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:

.

Часто вместо термина «плотность распределения вероятностей» используют термин «плотность вероятностей» или «дифференциальная функция».

Свойства плотности распределения:

1. Плотность вероятностей неотрицательна в любой точке оси :

 при .

2. Вероятность того, что непрерывная случайная величина  примет значение,

принадлежащее интервалу , определяется равенством:

.

3. Зная плотность вероятностей, можно найти функцию распределения:

.

4. Несобственный интеграл от плотности вероятностей в пределах от  до  равен

единице (условие нормировки):

.

5. Если все возможные значения случайной величины принадлежат интервалу , то

.

Определение 4. Математическое ожидание непрерывной случайной величины 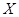, возможные значения которой принадлежат всей оси , определяется равенством

,

где  – плотность вероятностей случайной величины .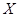

Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу , то

.

Математическое ожидание обладает следующими свойствами:

1. Математическое ожидание постоянной величины равно самой постоянной:

.

2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

 

.

3. Постоянный множитель можно выносить за знак математического ожидания:

.

4. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

.

Определение 5. Дисперсия непрерывной случайной величины 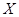, возможные значения которой принадлежат всей оси , определяется равенством:

.

Как и в случае с дискретной случайной величиной, справедлива теорема:

.

В частности, если все возможные значения  принадлежат интервалу , то

или

.

Дисперсия обладает следующими свойствами:

1. Дисперсия постоянной величины  равна нулю: 

.

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

.

3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:

.

4. Дисперсия произведения независимых случайных величин, математические ожидания которых равны нулю, равна произведению дисперсий сомножителей:

.

5. Дисперсия суммы постоянной и независимой случайной величины равна  дисперсии независимой случайной величины:

.

 

Пример. Дана функция распределения непрерывной случайной величины :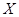

Требуется найти:

1. график функции распределения ,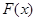

2. плотность ,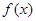

3. график плотности ,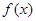

4. математическое ожидание ,

5. дисперсию ,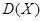

6. среднее квадратическое отклонение ,

7. вероятности .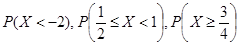

Решение.

1. Построим график функции распределения

2. Так как плотность  равна первой производной от функции распределения

,

то найдем производные от каждой из функций, составляющих функцию :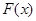

.

Тогда получаем функцию :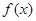

 

 

 

Рис. 2. График функции распределения.

 

3. Построим график плотности

Рис. 3. График плотности .

 

Заметим, что при  и  производная не существует.

4. Найдем математическое ожидание непрерывной случайной величины Х:

.

5. Чтобы найти дисперсию непрерывной случайной величины 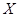, найдём математическое ожидание случайной величины :

.

Дисперсию найдем по формуле:

.

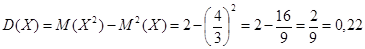6. Среднее квадратическое отклонение  найдем по формуле:

.

7. Найдем вероятность того, что случайная величина 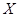 примет значение из интервала , то есть :

,

Вторую вероятность 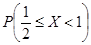 найдём по формуле

:

 

.

 

Так как события и 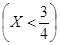 противоположные, то вероятность события  находится по формуле:

.