Числовые характеристики дискретной случайной величины

Определение 1. Математическим ожиданием дискретной случайной величины называется число, равное сумме произведений значений случайной величины на соответствующие вероятности их появления:

Если множество возможных значений случайной величины 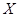счетное, то математическое ожидание определяется формулой

Математическое ожидание обладает следующимисвойствами:

1. Математическое ожидание постоянной величины равно самой постоянной:

2. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых (то же относится к разности):

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

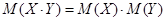4. Постоянный множитель можно выносить за знак математического ожидания:

Определение 2. Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений и соответствующих вероятностей:

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

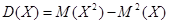Доказательство. Математическое ожидание есть постоянная величина, следовательно, и есть также постоянные величины. Приняв это во внимание и пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии:

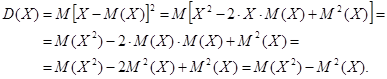
Итак,

Математическое ожидание квадрата дискретной случайной величины находится по формуле:

Среднее квадратическое отклонение определяется формулой .

Свойства дисперсии:

1. Дисперсия постоянной величины равна нулю:

2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

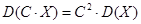3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

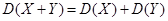4. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины:

Пример 1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

	–5	2	3	4
	0,4	0,3	0,1	0,2

Решение. Найдем математическое ожидание случайной величины :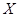

Дисперсию можно вычислить, исходя из ее определения, однако воспользуемся формулой:

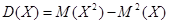которая быстрее ведет к цели.

Напишем закон распределения :

	25	4	9	16
	0,4	0,3	0,1	0,2

Найдем математическое ожидание :

Найдем искомую дисперсию:

Найдем искомое среднее квадратическое отклонение:

Определение 3. Дискретная случайная величина 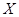, вероятности значений которой находятся по формуле Бернулли, называется распределённой по биномиальному закону. В таком случае говорят, что 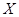имеет биномиальное распределение.

Теорема. Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины 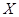, распределённой по биномиальному закону, вычисляются по формулам: