Эмпирическая функция распределения

Пусть известно статистическое распределение частот количественного признака 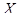. Введем обозначения:  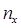 ─ число наблюдений, при которых наблюдалось значение признака меньше  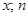– общее число наблюдений (объем выборки). Ясно, что относительная частота события  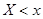равна 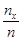. Если  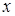изменяется, то, вообще говоря, изменится и относительная частота, то есть относительная частота  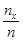есть функция от 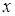. Так как статистическое распределение выборки находится эмпирическим (опытным) путем, то эту функцию называют эмпирической.

Определение 1. Эмпирической функцией распределения (функцией распределения выборки) называется функция 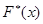, определяющая для каждого значения  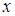относительную частоту события .

,

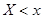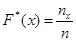где 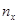 ─ число вариант, меньших  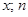– объем выборки.

В отличие от эмпирической функции распределения выборки функцию распределения 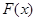 генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция 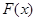определяет вероятность события 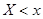, а эмпирическая функция  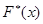определяет относительную частоту этого же события.

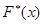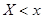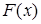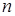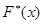Доказано, что относительная частота  события  стремится по вероятности к вероятности  этого события. Другими словами,  при больших значениях  числа  и 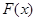 мало отличаются одно от другого в том смысле, что

.

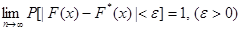 Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. Такое заключение подтверждается и тем, что 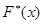обладает всеми свойствами .

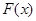Из определения функции 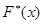 вытекают следующие ее свойства:

1) значения эмпирической функции принадлежит отрезку ;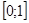

2) 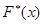– неубывающая функция;

3) если 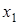 ─ наименьшая варианта, то  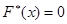при ;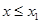

4) если 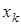 ─ наибольшая варианта, то  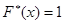при .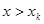

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построить эмпирическую функцию по данному распределению выборки:

Варианты	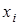2	6	10
Частоты	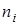12	18	30

Решение. Найдем объем выборки (сумма всех частот ):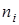

.

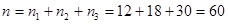1. Наименьшая варианта равна 2 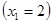, следовательно, 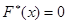, при 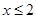 (по свойству 3 функции ).

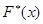2. Значения, меньшие 6 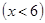, а именно 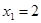, наблюдались  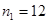раз, следовательно, 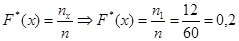,  при .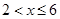

3.Значения 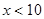, а именно  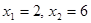наблюдались  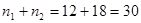раз, следовательно,  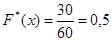,при .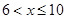

4. Так как 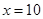 – наибольшая варианта, то 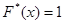, при 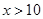 (по свойству 4 функции ).

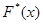Искомая эмпирическая функция имеет вид:

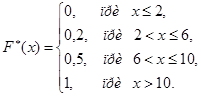
Ниже (рис. 5) приведен график полученной эмпирической функции.

На графике на соответствующих осях отложены значения функции

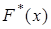 и значения вариант

Рис. 5. График эмпирической функции.