2020-04-07
103
Уравнение основного контура можно получить методом эталонного уравнения. Полагаем, что желаемая динамика системы описывается дифференциальным уравнением вида:
(4.17)
где 
– эталонное входное воздействие. Уравнение (4.17) получено согласно заданным показателям качества переходных процессов и описывает эталонную модель. В процессе синтеза адаптивного регулятора полного порядка используем уравнение объекта (4.9), разрешенное относительно старшей производной
. (4.18)
Согласно выбранному методу приравниваются правые части (4.17), (4.18), полученное уравнение разрешается относительно управляющей переменной, после чего выполняется замена неизвестных коэффициентов и функции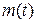 
соответствующими коэффициентами регулятора:
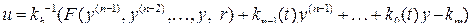, (4.19)
здесь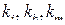 
- настраиваемые коэффициенты, i={0, 1,…,n-1}.
Пусть коэффициенты регулятора образуют вектор 
, размерности -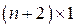 
, тогда алгоритм адаптации со старшей производной запишется в виде
(4.20)
или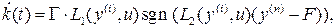 
(4.21)
где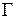 
– матрица коэффициентов передачи, 
; 
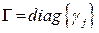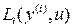– вспомогательные вектор-функции. Для сходимости процессов в системе (4.9), (4.19), (4.20) элементы вектор-функции 
определяются следующим образом:
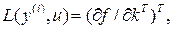(4.22)
где 
Таким образом, адаптивный регулятор описывается уравнениями
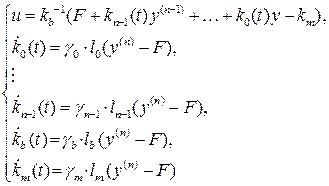(4.23)
Согласно (4.22) элементы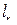 
вектор-функции имеют следующий вид:
Для реализации синтезированного закона управления (4.23) требуется информация о производных выходной переменной, оценку которых можно получить с помощью линейной малоинерционной динамической системы. Обычно такая система называется либо дифференцирующим фильтром, либо фильтром оценки производных (ФОП). Дифференциальное уравнение ФОП имеет вид:
,
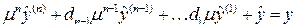где 
- оценка 
. С учетом фильтра оценки производных порядок адаптивной системы равен 
где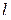 
- число контуров настройки коэффициентов адаптивного регулятора, 
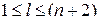, значение 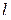зависит от количества неизвестных параметров и присутствия внешнего возмущения в объекте управления.
