МЕТОДИЧЕСКОЕ ПОСОБИЕ
КОНТРОЛЬНЫЕ РАБОТЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К НИМ
По дисциплине
«МАТЕМАТИКА»
Тюмень 2016
Содержание
| Введение……………………………………………………………. | 3 |
| Раздел 1 Основы дифференциального исчисления……………… | 4 |
| 1.1. Дифференцирование функций……………………………….. | 4 |
| 1.2. Механический смысл производной………………………….. | 7 |
| 1.3. Исследование функции и построение графиков……………. | 7 |
| Раздел 2 Основы интегрального исчисления……………………. | 9 |
| 2.1 Интегрирование функций……………………………………. | 9 |
| 2.2 Вычисление площади фигуры……………………………….. | 12 |
| Раздел 3 Задачи для контрольной работы……………………….. | 14 |
| Список использованных источников……………………………. | 20 |
Введение.
Данное методическое пособие содержит примеры решения заданий для выполнения контрольных работ, также дидактический материал курса «Математика» для студентов второго курса заочного отделения дистанционной формы обучения. В методическое пособие входит перечень заданий к домашней контрольной работе на 20 вариантов, в каждом варианте 5 заданий.
Раздел 1. Основы дифференциального исчисления
Дифференцирование функций
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
 . (1)
. (1)
Дифференцирование – это операция нахождения производной функции. Дифференцирование состоит из двух этапов:
1) применение правил дифференцирования;
1.  3.
3.  5.
5. 
2.  4.
4.  , где с-число.
, где с-число.
2) применение формул дифференцирования.
| Элементарные функции | Сложные функции | ||
| 1. |  где с-число где с-число
| ||
| 2. | 
| ||
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 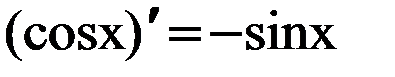
| 6. | 
|
| 7. | 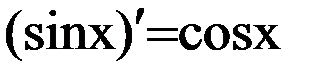
| 7. | 
|
| 8. | 
| 8. | 
|
| 9. | 
| 9. | 
|
| 10. | 
| 10. | 
|
| 11. | 
| 11. | 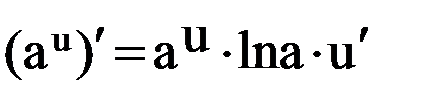
|
| 12. | 
| 12. | 
|
| 13. | 
| 13. | 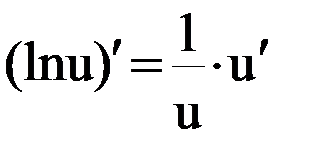
|
| 14. | 
| 14. | 
|
| 15. | 
| 15. | 
|
| 16. | 
| 16. | 
|
| 17. | 
| 17. | 
|
Пример 1. Найти производную функции  .
.
Применяем правило:  , получим:
, получим:  , т.к.
, т.к.  ;
;
Пример2. Найти производную функции  .
.
Применяем правило:  , получим:
, получим:  , т.к.
, т.к.  ;
;
Пример 3. Найти производную функции  .
.
Применяем правило:  , получим:
, получим:  , т.к.
, т.к.  ;
;
Пример 4. Найти производную функции  . Применяем правило:
. Применяем правило:  , получим:
, получим:  , т.к.
, т.к.  ;
;
Пример 5. Найти производную функции  . Применяем правило:
. Применяем правило:  , получим:
, получим:  , т.к.
, т.к.  ;
;
Пример 6. Найти производную функции  , получим:
, получим:  ;
;
Пример 7. Найти производную функции  . По формуле (4), получим:
. По формуле (4), получим: 
Пример 8. Найти производную функции  , получим:
, получим:  ;
;
Пример 9. Найти производную функции  , получим:
, получим:  ;
;
Пример 10. Найти производную функции  . По правилу
. По правилу  , получим:
, получим:  ;
;
Пример 11. Найти производную функции  . По правилу
. По правилу  получим
получим
 . По правилу
. По правилу  получим
получим
 . По формулам дифференцирования (4, 13, 7) получим
. По формулам дифференцирования (4, 13, 7) получим 
Пример 12. Найти производную функции  .
.
По правилу  получим
получим
 . По формулам дифференцирования (4, 11) получим
. По формулам дифференцирования (4, 11) получим 
Пример 13. Найти производную функции 
Применяем правило:  , получим:
, получим: 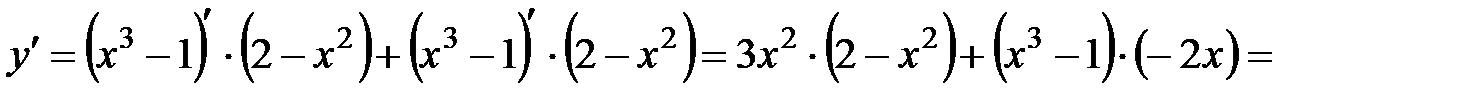
 ;
;
Пример 14. Найти производную функции 
По правилу 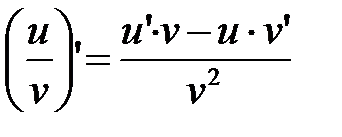 получим
получим  .
.
По формулам дифференцирования (6, 10) получим 
Пример 15. Найти производную функции 
Применяем правило: 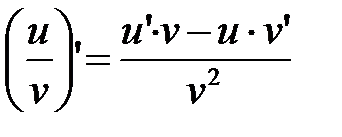 , получим:
, получим: 
 .
.
 2020-04-07
2020-04-07 151
151







