Совокупность всех первообразных для функции  или для дифференциала
или для дифференциала  называется неопределенным интегралом и обозначается:
называется неопределенным интегралом и обозначается:
 , (1)
, (1)
где  - подынтегральная функция;
- подынтегральная функция;  - подынтегральное выражение;
- подынтегральное выражение;  - произвольная постоянная.
- произвольная постоянная.
Основные свойства неопределенного интеграла.
1. 
2. 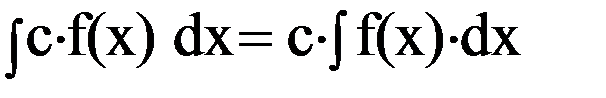 , где с-число.
, где с-число.
Таблица интегралов (первообразных):
| Элементарные функции: | Сложные функции: | ||
| 1. | 
| 1. | |
| 2. | 
| 2. | 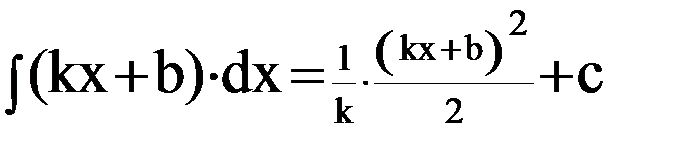
|
| 3. |  , где n ≠ -1 , где n ≠ -1
| 3. | 
|
| 4. | 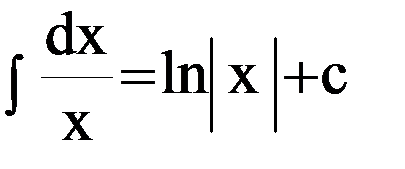
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 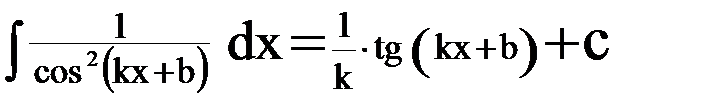
|
| 8. | 
| 8. | 
|
| 9. | 
| 9. | 
|
| 10. | 
| 10. | 
|
| 11. | 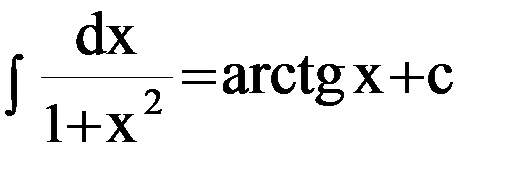
| 11. | 
|
| 12. | 
| 12. | 
|
| 13. | 
| 13. | 
|
| 14. | 
| 14. | 
|
Пример 1: Вычислите интеграл:  .
.
Решение: По правилу  получим
получим 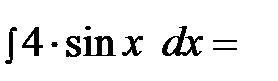
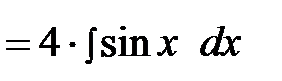 . По формуле (6) получим
. По формуле (6) получим 
 .
.
Пример 2: Вычислите интеграл:  .
.
Решение: По формуле (15) получим 

Пример 3: Вычислите интеграл:  .
.
Решение: Распишем дробь на два слагаемых  . По правилу
. По правилу 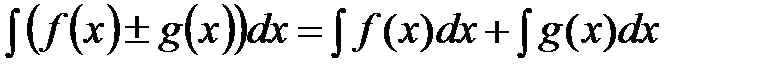 получим
получим
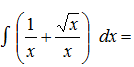
 .
.
По свойству степеней  , получаем
, получаем  . По формулам (3, 4), получим
. По формулам (3, 4), получим 
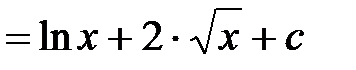 .
.
|
|
|
Пример 4: Вычислите интеграл:  .
.
Решение: Выполним замену, получим:

Здесь использовали формулу 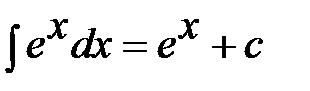
Вычисление определенных интегралов непосредственно.
Пример 5. 
Пример 6. 
Вычисление площади фигуры
Определенный интеграл есть площадь криволинейной трапеции (рисунок 9), ограниченной снизу – осью OX, сверху кривой y=f(x), слева и справа – прямыми x=a, x=b.
Пример 7: Найти площадь фигуры, ограниченной линиями: y=2x+4, y=0, x=1, x=-1
Таблица 9 – Точки прямой
| X | 0 | -2 |
| y | 4 | 0 |
Решение: y=2x+4 – прямая. Для построения прямой необходимо найти две точки (таблица 9).


а)  б)
б) 

в) 
Рисунок 9 – Графики функций
y=0 – ось OX, x=1, x= -1 – прямые параллельные OY. Строим все линии на рисунке 10. 


Рисунок 10 – график функции
Пример 8: Найти площадь фигуры, ограниченной линиями: y=x2, y=2x
Решение: y=x2 – парабола, ветви вверх.
Для построения параболы необходимо найти точки (таблица 10).
| X | -2 | -1 | 0 | 2 | 1 |
| y | 4 | 1 | 0 | 4 | 1 |
Таблица 10 – Точки параболы
y=2x – прямая.
Для построения прямой необходимо найти две точки (таблица 11).
| X | 0 | 2 |
| y | 0 | 4 |
Таблица 11 – Точки прямой
Найдем a и b: x2=2x, x2-2x=0, x(x-2)=0, x=0, x=2; следовательно a=0, b=2. Построим графики функций на рисунке 11.

Рисунок 11 – График функции
 ,
,  ,
,


Ответ. 
Раздел 3. Задания для контрольной работы.
Задание1: Вычислить производную функций.
Вариант № 1, 11.
1.  , 2.
, 2. 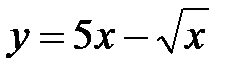 , 3.
, 3.  , 4.
, 4. 
5.  , 6.
, 6.  , 7.
, 7. 
Вариант № 2, 12.
1.  , 2.
, 2.  , 3.
, 3.  , 4.
, 4. 
5.  , 6.
, 6.  , 7.
, 7. 
|
|
|
Вариант № 3, 13.
1.  , 2.
, 2.  , 3.
, 3.  ,
,
4.  , 5.
, 5.  , 6.
, 6.  , 7.
, 7. 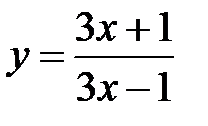
Вариант № 4, 14.
1.  , 2.
, 2.  , 3.
, 3. 
4.  , 5.
, 5. 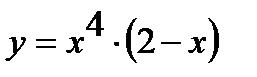 , 6.
, 6.  , 7.
, 7. 
Вариант № 5, 15.
1.  , 2.
, 2.  , 3.
, 3. 
4.  , 5.
, 5.  , 6.
, 6.  , 7.
, 7. 
Вариант № 6, 16.
1.  , 2.
, 2. 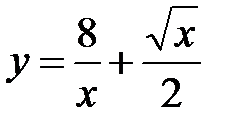 , 3.
, 3. 
4.  , 5.
, 5.  , 6.
, 6.  , 7.
, 7. 
Вариант № 7, 17.
1.  , 2.
, 2.  , 3.
, 3. 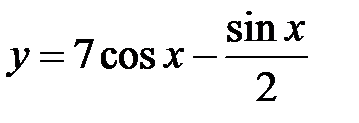
4.  , 5.
, 5.  , 6.
, 6.  , 7.
, 7. 
Вариант № 8, 18.
1. 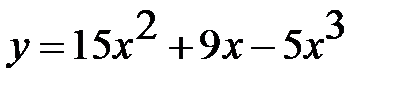 , 2.
, 2.  , 3.
, 3. 
4.  , 5.
, 5.  , 6.
, 6.  , 7.
, 7. 
Вариант № 9, 19.
1.  , 2.
, 2.  , 3.
, 3. 
4.  , 5.
, 5.  , 6.
, 6.  , 7.
, 7. 
Вариант № 10, 20.
1.  , 2.
, 2.  ,.
,. 
4.  , 5.
, 5.  , 6.
, 6. 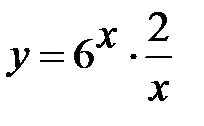 , 7.
, 7. 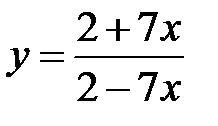
Задание 2. Дан закон движения точки:  . Найти: 1) формулы скорости и ускорения; 2) значения скорости и ускорения в момент времени
. Найти: 1) формулы скорости и ускорения; 2) значения скорости и ускорения в момент времени  .
.
1 вариант. 
2 вариант. 
3 вариант. 
4 вариант. 
5 вариант. 
6 вариант. 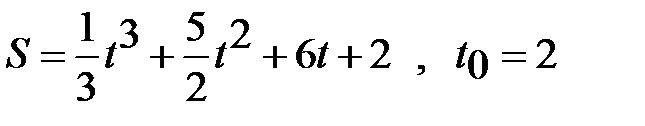
7 вариант. 
8 вариант. 
9 вариант. 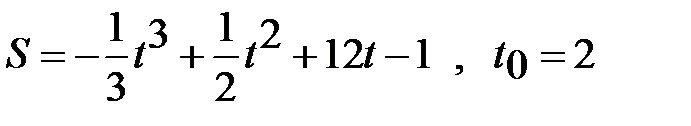
10 вариант. 
11 вариант. 
12 вариант. 
13 вариант. 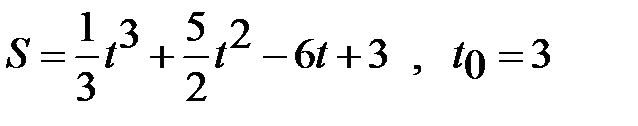
14 вариант. 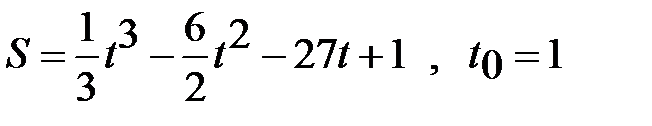
15 вариант. 
16 вариант. 
17 вариант. 
18 вариант. 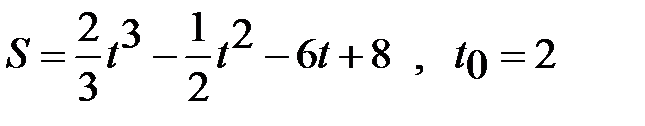
19 вариант. 
20 вариант. 
Задание 3. Исследовать функцию и построить график:
1 вариант:  ;
;
2 вариант: 
3 вариант:  ;
;
4 вариант: 
5 вариант: 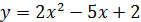 ;
;
6 вариант:  ;
;
7 вариант:  ;
;
8 вариант:  ;
;
9 вариант:  ;
;
10 вариант: 
11 вариант:  ;
;
12 вариант: 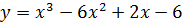 ;
;
13 вариант:  ;
;
14 вариант: 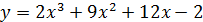 ;
;
15 вариант:  ;
;
16 вариант:  ;
;
17 вариант:  ;
;
18 вариант:  ;
;
19 вариант:  ;
;
20 вариант:  .
.
 2020-04-07
2020-04-07 100
100








