Компоненты перемещений и деформаций в

ЭЛЕМЕНТАРНОМ ОБЪЕМЕ

Если тело деформируется, то каждая его точка смещается от первоначального положения. При этом подразумевается, что тело находится в равновесии и не имеет возможности перемещаться как целое. Таким образом, считается, что перемещение каждой точки происходит исключительно вследствии деформации.

Пусть координаты точки в начальный момент x, y, z, а в данный момент деформации (близкий к начальному) x^', y^', z^', тогда

x^' – x = u_x;

y^' – y = u_y;

z^' – z = u_z,

представляют собой проекции перемещения на координатные оси, т.е. являются компонентами перемещения точки.

*Аддитивность – свойство физических, геометрических и других величин, состоящее в том, что значение величин, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разделении объекта на части.

Для различных точек компоненты перемещения различны, и они и их производные являются непрерывными функциями координат.

Элементарный прямоугольный параллелепипед, мысленно выделенный в теле, при деформации последнего изменит не только свое положение, но и свою форму. В общем случае ребра параллелепипеда изменяют длину, а углы перестанут быть прямыми. Получим деформации двух видов: линейные (удлинения) и угловые (сдвиги).

Относительные линейные деформации обозначим ε с индексами, подобными принятым для напряжений σ. Относительные сдвиги обозначим γ с двумя индексами, указывая этими индексами координатную плоскость, на которую проецируется искажаемый деформацией угол. При этом относительные сдвиги считаются положительными, если им соответствует уменьшение угла со сторонами, направленными в положительном направлении координатных осей. Сказанное поясняет рис. 2.3.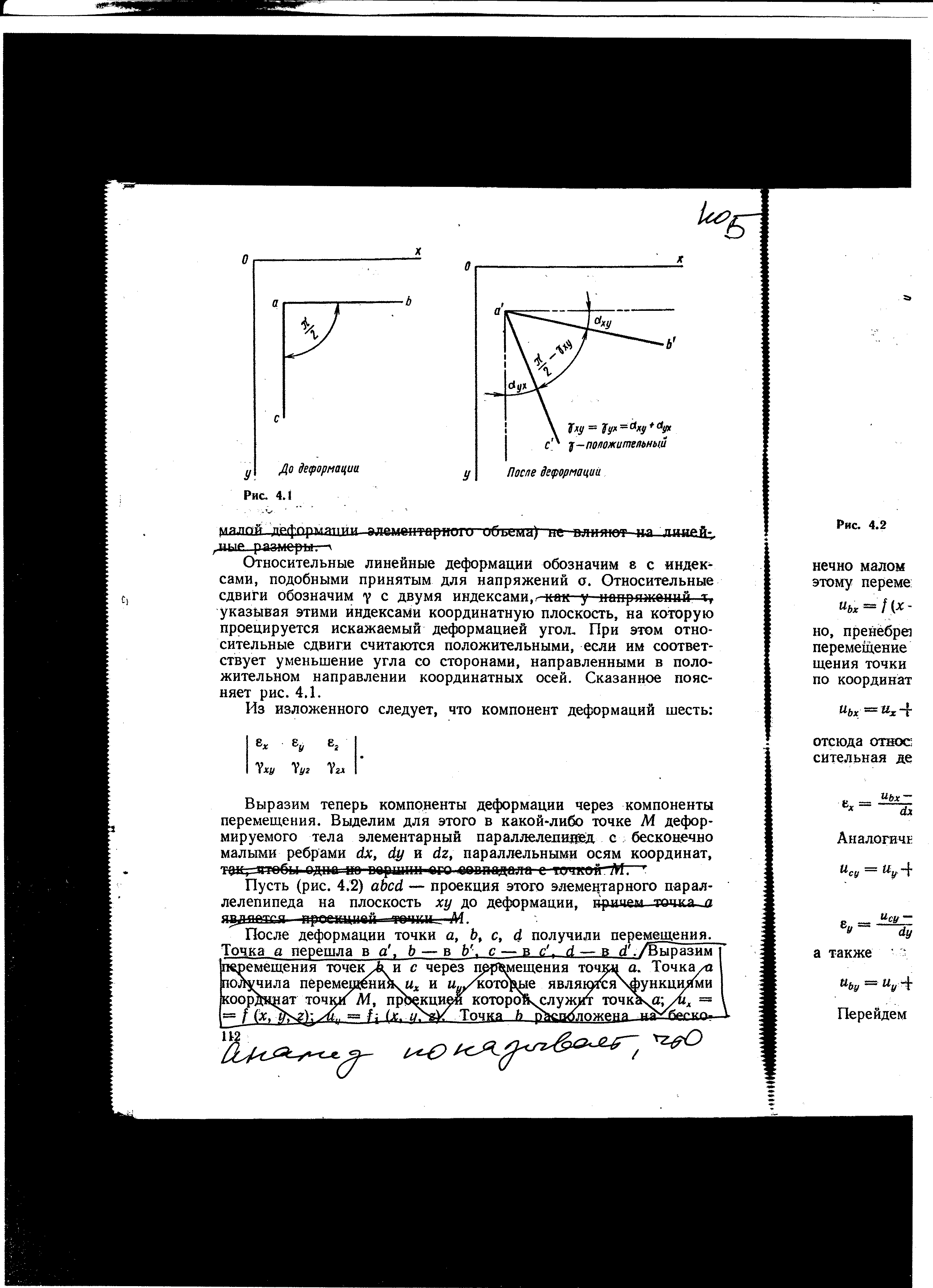

Рис. 2.3.

Из изложенного следует, что компонент деформаций шесть:

.

Выразим теперь компоненты деформации через компоненты перемещений. Выделим для этого, в какой – либо точке М деформируемого тела элементарный параллелепипед с бесконечно малыми ребрами dx, dy и dz, параллельными осям координат.

Пусть (рис. 2.4) abcd – проекция этого элементарного параллелепипеда на плоскость xy до деформации.

После деформации точки a, b, c, d получили перемещения. Точка a перешла в a^', b – в b^', c – в c^', d – в d^'. Анализ показывает, что

относительная деформация ε в направлении x, .

Аналогично получим .

Рис. 2.4.

Проецируя рассматриваемый параллелепипед на плоскости yz и zx, найдем выражения других компонент деформации.

В итоге получим:

 компоненты тензора деформаций (2.15)

Эти уравнения получил О. Л. Коши.

Таким образом, если движение тела определено функцией перемещения и, то показатели деформации ε, γ в направлении координатных осей легко вычислить по уравнению (2.15).