Тензорные характеристики деформации

Для полной характеристики деформации в общем случае необходимо иметь функции компонент перемещения (2.9) и вычислить девять их производных. Производные du_x / dx, du_y/dy и т.д. образуют так называемый тензор единичного относительного перемещения:

. (2.16)

В общем случае этот тензор несимметричен относительно главной диагонали. Представим его в виде суммы симметричного и кососимметричного тензора

(2.17)

Тензор Т_ε называется тензором деформации, или тензором чистой деформации; тензор Т_ω – тензором поворота, или тензором вращения.

Тензоры Т_ε, Т_ω можно представить в компактном виде:

(2.18)

ω_xy = du_x/dy

В курсах теории упругости и пластичности показано, что при изменении положения координатных осей одно и то же деформированное состояние выражается различными тензорами Т_ε, компоненты которых при повороте координатных осей монотонно изменяются, достигая максимума или минимума. При определенном положении координатных осей тензор Т_ε может иметь форму

Тензор – это геометрический объект, с многомерным массивом, т.е. набором чисел, занумерованных несколькими индексами (иначе говоря – н-мерной таблицей).

Тензор – это объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого.

. (2.19)

Тензор, у которого γ_xy = γ_yz = γ_zx = γ_xz = γ_zy = γ_yx = 0 называется тензором главных деформаций. Координатные оси, по которым компоненты тензора деформаций γ_xy, γ_yz, γ_zx обращаются в нуль, называются главными осями тензора деформаций. Особенность главных осей состоит в том, что линейные элементы, ориентированные вдоль этих осей до начала деформаций, остаются взаимно перпендикулярными и в процессе малой деформации, и после завершения его. Компоненты тензора деформаций ε₁, ε₂, ε₃ в направлении главных осей называются главными деформациями. Особенность главных деформаций состоит в том, что одна из них наибольшая, другая – наименьшая из всех возможных, взятых в окресности данной точки по любому произвольному направлению. Чтобы определить главные деформации необходимо решить кубическое уравнение:

ε³ – I₁(Т_ε) ε²+ I₂(Т_ε) ε – I₃(Т_ε) = 0. (2.20)

Здесь I₁(Т_ε), I₂(Т_ε), I₃(Т_ε) – коэффициенты, инвариантные к преобразованию координат, составленные из компонентов тензора деформаций Т_ε:

(2.21)

Эти коэффициенты носят название инвариантов тензора деформаций Т_ε. Корни уравнения (2.21) – это главные деформации. В курсах теории упругости и пластичности доказано, что все корни уравнения (2.21) действительные. Значит, в любой точке деформированного тела есть главные оси, вдоль которых деформация определяется компонентами ε₁, ε₂, ε₃, а сдвиги по этим осям отсутствуют (γ_xy = γ_yz = γ_zx = 0). Первый инвариант тензора деформаций имеет определенный физический смысл: он выражает относительное изменение объема деформируемого тела или его элемента. При пластической деформации объем тела или его элемента не изменяется:

(2.22)

Это равенство принято называть законом или условием постоянства объема. Условие (2.22) можно представить и в дифференциальной форме, если вместо компонент тензора деформаций взять их значения по уравнениям Коши (2.15), (2.16):

(2.23)

Тензор характеризует полную деформацию тела: он определяет изменение формы тела (компоненты ε, γ) и объема (компоненты ε). Чтобы разделить эти виды деформации тензор раскладывают на два тензора

, где

(2.24)

Тензор называют шаровым тензором деформации. Его особенность заключается в том, что компоненты γ равны нулю, а диагональные компоненты равны средней деформации. Для пластической деформации . Следовательно, и объем деформируемого тела не изменяется. Тензор называется девиатором деформации. Его важная особенность состоит в том, что . Это означает, что девиатор деформации характеризует только изменение формы тела. Для пластической деформации , поэтому 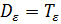. Исключительно важную роль играет в ТОМД второй инвариант девиатора деформации . Функция