§ 1. Поступательное и вращательное движение
В предыдущих лекциях мы познакомились с механикой материальной точ- ки. Использование модели материальной точки позволило нам сравнительно простыми средствами описать состояние материальной точки в любой момент времени и изменение этого состояния со временем (см. лекцию № 3, § 3 и вы- вод 7 из лекции № 3).
Модель абсолютно твердого тела (см. лекцию № 1, § 1) расширяет наши возможности и позволяет ввести различие между поступательным и враща- тельным движением.
Поступательным движением называется такое движение, при котором любая линия, проведенная в теле, остается параллельной самой себе.
Вращательным движением называется такое движение, при котором каждая точка твердого тела движется по своей окружности, центры всех окружностей лежат на одной прямой, называемой осью вращения.
На рис. 7.1а, 7.1б проиллюстрировано это различие. Отметим, что если на этих рисунках заменить изображенное затененным овалом твердое тело на ма- териальную точку, расположенную в центре масс тела, то различие между по- ступательным и вращательным движением исчезает. Более того, если ось вра- щения проходит через центр масс тела, то при использовании модели матери- альной точки говорить о вращении точки вокруг оси, проходящей через эту точку, не имеет никакого смысла.
 Поступательное движение (рис. 7.1а). Любая линия, проведенная в твер- дом теле, при движении остается параллельной самой себе.
Поступательное движение (рис. 7.1а). Любая линия, проведенная в твер- дом теле, при движении остается параллельной самой себе.
В данном примере траектория центра масс – окружность, остальные точки тела также движутся по окружностям, но центры этих ок- ружностей не лежат на одной прямой.
Рис. 7.1а 57
Вращательное движение (рис. 7.1б). Центр масс движется по окружности
 того же радиуса. Каждая точка твердого тела движется по своей окружности; цен- тры всех окружностей лежат на прямой, называемой осью вращения.
того же радиуса. Каждая точка твердого тела движется по своей окружности; цен- тры всех окружностей лежат на прямой, называемой осью вращения.
Здесь, как и в предыдущем примере, центр масс тела движется по той же ок- ружности.
Рис. 7.1б
§ 2. Псевдовектор бесконечно малого поворота
Любое движение твердого тела можно разложить на поступательное и вращательное. Например, движение Земли состоит из поступательного движе- ния по эллиптической траектории вокруг Солнца и вращательного движения вокруг собственной оси. При изучении поступательного движения в большин-

 стве случаев можно использовать модель матери- альной точки. При изучении вращательного дви- жения используют модель абсолютно твердого те- ла. При этом, в случае закрепленной оси вращения, положение абсолютно твердого тела в пространст- ве можно задать всего лишь одной переменной – зависящим от времени углом поворота (t). Ока- зывается, бесконечно малым углам поворота мож- но придать векторный характер, при этом направле- ние вектора связывают с направлением вращения.
стве случаев можно использовать модель матери- альной точки. При изучении вращательного дви- жения используют модель абсолютно твердого те- ла. При этом, в случае закрепленной оси вращения, положение абсолютно твердого тела в пространст- ве можно задать всего лишь одной переменной – зависящим от времени углом поворота (t). Ока- зывается, бесконечно малым углам поворота мож- но придать векторный характер, при этом направле- ние вектора связывают с направлением вращения.
Векторы, направления которых связываются с направлением вращения, называются псевдовекто- рами.
При повороте тела на угол 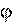 вводят псевдо- вектор бесконечно малого поворота
вводят псевдо- вектор бесконечно малого поворота 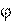 . В правой системе координат направление
. В правой системе координат направление 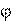 определяют правилом правого винта: винт, расположенный вдоль оси, вращается вместе с телом, направление
определяют правилом правого винта: винт, расположенный вдоль оси, вращается вместе с телом, направление
Рис. 7.2
его поступательного движения определяет на-
правление псевдовектора (рис. 7.2).
В левой системе координат направление псевдовектора изменится на об- ратное, истинный вектор при этом не меняет направления.
Модуль псевдовектора 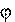 равен величине угла поворота.
равен величине угла поворота.
§ 3. Угловая скорость и угловое ускорение
Угловая скорость и угловое ускорение вводятся с помощью определений, аналогичных определениям скорости (2.1) и ускорения (2.7).
Угловая скорость
 Угловой скоростью называется векторная величи- на, равная первой производной угла поворота тела по времени.
Угловой скоростью называется векторная величи- на, равная первой производной угла поворота тела по времени.

 , или . (7.1)
, или . (7.1)
Рис.
Угловое ускорение
Псевдовектор 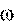 направлен по оси вращения так же, как и псевдовектор
направлен по оси вращения так же, как и псевдовектор 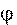 (рис. 7.3).
(рис. 7.3).
 Радиан – единица измерения угла – величина без-
Радиан – единица измерения угла – величина без-
размерная (см. на рис. 3.2), поэтому из (7.1) следу- ет, что угловая скорость измеряется в рад/с или в с-1.
Угловым ускорением 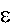 называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла пово- рота по времени.
называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла пово- рота по времени.
 . (7.2)
. (7.2)
Из (7.2) следует, что размерность углового ускорения
[ . Из опре-
 деления (7.2) следует, что угловое ускорение является псевдовектором.
деления (7.2) следует, что угловое ускорение является псевдовектором.
В случае закрепленной оси вращения направление углового ускорения совпадает с направлением угловой скорости при ускоренном движении и про- тивоположно при замедленном.
§ 4. Связь угловых и линейных кинематических величин
Абсолютно твердое тело можно рассматривать как систему материальных точек с неизменными расстояниями между ними. Эти точки при вращательном движении движутся по окружностям, центры которых лежат на оси вращения (см. рис. 7.1б). Линейные скорости v точек твердого тела и их линейные уско- рения a связаны с угловыми кинематическими величинами ω и ε, а также за-
висят от расстояния R материальной точки до оси вращения.

 Найдем связь линейной скорости материальной точки твердого тела и угловой скорости. Из определе- ния радианной меры угла следует связь бесконечно малого отрезка пути ds материальной точки, удален- ной от оси вращения на расстояние R с углом поворо- та d (рис. 7.4, а также см. рис. 3.2). Используя эту связь и определение модуля линейной скорости (2.3), получим:
Найдем связь линейной скорости материальной точки твердого тела и угловой скорости. Из определе- ния радианной меры угла следует связь бесконечно малого отрезка пути ds материальной точки, удален- ной от оси вращения на расстояние R с углом поворо- та d (рис. 7.4, а также см. рис. 3.2). Используя эту связь и определение модуля линейной скорости (2.3), получим:
откуда
ds R d


 dt dt
dt dt
,

 . (7.3)
. (7.3)
Рис. 7.4
Формула (7.3) выражает связь между модулями линейной и угловой скорости: линейная скорость
равна угловой, умноженной на радиус окружности, по которой движется мате- риальная точка.
В векторном виде связь
v и 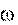 записывается следующим образом:
записывается следующим образом:

v , (7.4)

здесь квадратные скобки обозначают векторное произведение векторов
И R.
Направление векторного произведения определяется по правилу правого винта:
 а) винт устанавливают перпендикулярно перемножаемым векторам (у нас
а) винт устанавливают перпендикулярно перемножаемым векторам (у нас
это
и R);
б) винт вращают от первого вектора ко второму по кратчайшему расстоя-

нию (у нас – от и R);
в) направление поступательного движения винта укажет направление векторного произведения (у нас – направление вектора v).
Модуль векторного произведения:

 где – угол между векторами
где – угол между векторами
v

 и R.
и R.
R sin


 Если = 90, то sin = 1, и связь между модулями линейной и угловой скорости дается формулой:
Если = 90, то sin = 1, и связь между модулями линейной и угловой скорости дается формулой:

совпадающей с формулой (7.3).
Связь модуля линейного ускорения материальной точки твердого тела с угловой скоростью и угловым ускорением найдем, если продифференцируем по времени формулу (7.3):

 (v R
(v R
) t,
 dv R d,
dv R d,
dt dt
так как
dv (см. (3.3а)), то, используя (7.2), получим:
 dt
dt
В векторной форме:
. (7.5)




R
a . (7.5а)
 Формула (7.5а) дает связь тангенциального ускорения a с угловым
Формула (7.5а) дает связь тангенциального ускорения a с угловым 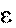 .
.
Найдем связь нормального ускорения с угловой скоростью.
2

 Так как v
Так как v
R
an (3.4а), заменяя в этой формуле
v на
R из (7.3), получим
связь нормального ускорения a n
с угловой скоростью

 . (7.6)
. (7.6)
 В векторном виде:
В векторном виде:
a n
(7.7)
Знак «минус» указывает на то, что векторы an и R
ные направления.
имеют противополож-
§ 5. Решение основной задачи механики для вращательного движения тела с закрепленной осью

 При вращательном движении положение абсолютно твердого тела задается зависимостью угла поворота от времени t. В случае равномерного вращения
При вращательном движении положение абсолютно твердого тела задается зависимостью угла поворота от времени t. В случае равномерного вращения
 ( const )
( const )
и равноускоренного вращения (
const) такая зависимость может
быть найдена по аналогии с равномерным (см. лекцию № 2, § 2) и равноуско- ренным движением материальной точки (см. лекцию № 3, § 2 и формулы (3.6) и (3.7)).
Рассмотрим сначала равномерное вращение. Запишем следствие из опре- деления (7.1) угловой скорости 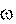 в следующем виде:
в следующем виде:
 (7.1а)
(7.1а)
 здесь мы опустили знаки векторов, т.к. ось вращения закреплена.
здесь мы опустили знаки векторов, т.к. ось вращения закреплена.
При = const интегрирование формулы (7.1а), выполненное аналогично интегрированию формулы (2.3а) в лекции № 2, § 2 дает следующий результат:



 (7.8)
(7.8)
здесь имеем:
– значение угла поворота в начальный момент времени. При 0 0

 (7.8а)
(7.8а)
Формула (7.8а) аналогична формуле (2.5), по которой находится путь при равномерном движении материальной точки.

 Периодом равномерного вращения Т называют время одного оборота. Так как в одном обороте 2 радиан, то из (7.8а) получим связь угловой скорости с периодом Т:
Периодом равномерного вращения Т называют время одного оборота. Так как в одном обороте 2 радиан, то из (7.8а) получим связь угловой скорости с периодом Т:


 откуда:
откуда:
2 . (7.9)


|
.


 Из (7.9) и (7.10) следует связь и
Из (7.9) и (7.10) следует связь и

(7.10)
(7.11)
 Для произвольного вращательного движения с переменным угловым уско- рением (t) зависимость скорости от времени находится интегрированием функции (t):
Для произвольного вращательного движения с переменным угловым уско- рением (t) зависимость скорости от времени находится интегрированием функции (t):

 t
t
0 (t)dt.
0
(7.12)
 Затем, интегрируя найденную функцию (t) (7.12), можно найти зависи- мость угла поворота от времени:
Затем, интегрируя найденную функцию (t) (7.12), можно найти зависи- мость угла поворота от времени:

 t
t
0 (t)dt.
0
(7.13)
Задача нахождения зависимости углового ускорения от времени выходит за рамки кинематики. Она решается в рамках динамики вращательного движе- ния.
 Для равноускоренного вращения (выводе формул (3.6) и (3.7), получим:
Для равноускоренного вращения (выводе формул (3.6) и (3.7), получим:

const),
действуя так же, как и при
 (7.14)
(7.14)
здесь
,
– 


 начальная угловая скорость;
начальная угловая скорость;
–  начальный угол поворота.
начальный угол поворота.
ИТОГИ ЛЕКЦИИ № 7
(7.15)
1. При изучении вращательного движения используют модель абсолютно твердого тела, позволяющую ввести различие между поступательным и враща- тельным движением (§ 1).
2. 
 Положение вращающегося тела определяется зависимостью от времени одной переменной – угла поворота
Положение вращающегося тела определяется зависимостью от времени одной переменной – угла поворота
3. Бесконечно малому углу поворота d можно придать в соответствии с
правилом правого винта векторный характер – ввести псевдовектор бесконечно
 малого поворота d
малого поворота d
4. Угловая скорость 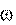 (7.1) вводится как производная по времени от угла
(7.1) вводится как производная по времени от угла
 поворота. Направлен вектор
поворота. Направлен вектор 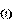 так же, как и псевдовектор d
так же, как и псевдовектор d
 .
.
5. Угловое ускорение (7.2) вводится как производная угловой скорости  по времени:
по времени:
 .
.
Угловая скорость равна второй производной угла поворота по времени:
 .
.
6.  Линейная скорость v материальной точки твердого тела связана с его угловой скоростью равенством (7.3):
Линейная скорость v материальной точки твердого тела связана с его угловой скоростью равенством (7.3):
 |
где R – расстояние от точки до оси вращения.
7.  Для тангенциального a и нормального a n
Для тангенциального a и нормального a n
ускорения материальной
 точки твердого тела справедливы формулы (7.5) и (7.6):
точки твердого тела справедливы формулы (7.5) и (7.6):
 |
a n R.
8. 


|


9.  При равноускоренном вращении угловая скорость и угол поворота
При равноускоренном вращении угловая скорость и угол поворота  следующим образом зависят от времени (7.14) и (7.15):
следующим образом зависят от времени (7.14) и (7.15):
 |  |
здесь
,




 и – начальные значения угловой скорости и угла поворота.
и – начальные значения угловой скорости и угла поворота.
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ЛЕКЦИЯ № 8
Момент силы и момент инерции
§ 1. Работа при вращательном движении. Момент силы

 д и с к R
д и с к R
d
ds R d


 F
F
Рис. 8.1
 На рис. 8.1 приведен самый простой пример вращения твердого тела при действии внешней силы. Тело представляет собою диск, который может вра- щаться вокруг неподвижной оси Z, проходящей через его центр перпендику- лярно рисунку. Внешняя сила F направлена по касательной к диску (такую си- лу можно создать с помощью нити, намотанной на диск).
На рис. 8.1 приведен самый простой пример вращения твердого тела при действии внешней силы. Тело представляет собою диск, который может вра- щаться вокруг неподвижной оси Z, проходящей через его центр перпендику- лярно рисунку. Внешняя сила F направлена по касательной к диску (такую си- лу можно создать с помощью нити, намотанной на диск).


 Найдем работу dA, совершаемую силой F при повороте диска на угол d
Найдем работу dA, совершаемую силой F при повороте диска на угол d 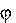 . В соответствии с (5.4): dA = Fsds, у нас Fs равна F. Величину ds выразим через d (см. рис. 8.1), воспользовавшись определением радианной меры угла. В результате получим:
. В соответствии с (5.4): dA = Fsds, у нас Fs равна F. Величину ds выразим через d (см. рис. 8.1), воспользовавшись определением радианной меры угла. В результате получим:
итак:
dA = F ds = F Rd zd




 dA =
dA =
(8.1)
 Здесь мы ввели новую величину z, являющуюся мерой внешнего воздей- ствия при вращательном движении:
Здесь мы ввели новую величину z, являющуюся мерой внешнего воздей- ствия при вращательном движении:
|


 Величина z называется моментом силы F относительно оси вращения Z. Формулу (8.2) можно записать в векторном виде:
Величина z называется моментом силы F относительно оси вращения Z. Формулу (8.2) можно записать в векторном виде:
. (8.3)
Векторное произведение векторов
R и Fτ
направлено вдоль оси враще-
ния Z в соответствии с правилом правого винта, введенным в § 3 лекции № 7. При произвольном направлении внешней силы F направление векторного про-
изведения
R на F
может не совпадать с осью вращения. В этом случае вектор
 Mz определяется как составляющая вектора M [ RF ], направленная вдоль
Mz определяется как составляющая вектора M [ RF ], направленная вдоль
оси вращения. Отметим, что модуль вектора R равен расстоянию от точки при- ложения силы до оси вращения.
В механике вводят также понятие вектора момента силы относительно произвольной точки О в соответствии со следующим определением:

M [ rF ], (8.4)
здесь r – вектор, проведенный из точки О в точку приложения силы (радиус- вектор).
Следовательно, момент силы относительно точки равен векторному произ- ведению радиус-вектора на вектор силы.
Можно показать, что если точка О расположена на оси вращения (в лю-
бом месте этой оси), то момент Mz
силы F относительно оси вращения Z бу-
дет равен проекции вектора M из (8.4) на эту ось.

 На рис. 8.2 это иллюстрируется для частного случая, когда сила F = F, т.е. не имеет составляющих вдоль оси Z и
На рис. 8.2 это иллюстрируется для частного случая, когда сила F = F, т.е. не имеет составляющих вдоль оси Z и
вектора R (проекции моментов этих со- ставляющих на ось z равны нулю, поэтому мы их не рассматриваем).

 В соответствии с формулой (8.4), примененной для нашего случая, модуль
В соответствии с формулой (8.4), примененной для нашего случая, модуль
вектора M – момента силы относительно точки О:






M = r × Fτ.
Рис. 8.2
Спроектируем вектор M на ось Z, тогда из рис. 8.2 видно, что:

 Mz = M ×cosβ,
Mz = M ×cosβ,
используя предыдущую формулу, получим:

Mz r

 Fτ cosβ.
Fτ cosβ.


 В соответствии с правилом определения направления векторного произведе-
В соответствии с правилом определения направления векторного произведе-

 ния (§ 3, лекция № 6), вектор M перпендикулярен вектору и cos = sin, следовательно:
ния (§ 3, лекция № 6), вектор M перпендикулярен вектору и cos = sin, следовательно:
r, значит, + = 90


Mz F
sin.






|
M z
что совпадает с формулой (8.2).
§ 2. Кинетическая энергия при вращательном движении. Момент инерции
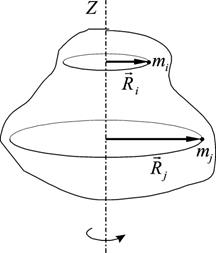
Как уже отмечалось (см. лекцию № 7, § 4), абсолютно твердое тело можно рассматривать как систему материальных точек с неизменными расстояниями между ними. Кинетическую энергию вращающегося тела можно найти как сумму кинетических энергий (5.8) всех материальных точек, составляющих
данное тело. Скорости этих точек vi
в соответствии с формулой (7.3), связаны

|
|
|

|
W = i i =
mR 2 ω 2 ω
m R2 .
|
i=1
i=1
2 2 i=1 i i
Введем новую величину
тельном движении:
Рис. 8.3
Iz, являющуюся мерой инертности при враща-
 . (8.5)
. (8.5)
Величина Iz
оси Z.
называется моментом инерции твердого тела, относительно
Таким образом:
Izω2
 Wк = 2. (8.6)
Wк = 2. (8.6)
Величину, стоящую под знаком суммы в формуле (8.6) называют момен- том инерции материальной точки относительно оси z:
 Izi
Izi
(8.7)
Следовательно, момент инерции материальной точки равен произведению массы этой точки на квадрат ее расстояния до оси вращения.
Таким образом, момент инерции твердого тела равен сумме моментов инерции всех материальных точек, составляющих это тело:
 Iz = Izi. (8.8)
Iz = Izi. (8.8)
i=1
Как видно из формулы (8.5), величина момента инерции материальной
точки
Izi
может быть разной для материальных точек с одинаковыми массами
mi вследствие возможного различия расстояний Ri
от этих точек до оси вра-
щения. Из формул (8.5), (8.7) и (8.8) следует, что величина момента инерции
твердого тела Iz
оси вращения.
зависит от распределения масс в твердом теле и от положения
При непрерывном распределении массы величина
mi в формуле (8.5) заме-
няется на бесконечно малую массу dm, а сумма заменяется на интеграл, кото- рый берется по всему объему тела:

|
(8.9)
При вычислении момента инерции величину dm выражают через плот- ность тела и бесконечно малый объем dV:
 dm dV.
dm dV.
(8.10)
Подставляя (8.10) в (8.9), получим формулу, решающую в общем виде за- дачу о нахождении момента инерции тела относительно заданной оси:

|
(8.11)
Теорема Штейнера
Для симметричных тел вычисления по формуле (8.11) значительно упро- щаются, если ось вращения проходит через центр масс тела. Обозначим момент инерции твердого тела относительно оси ОО, проходящей через центр масс, че-
рез I0
(рис. 8.4). Тогда для нахождения момента инерции относительно произ-
вольной оси O / O /, параллельной оси ОО и удаленной от нее на расстояние а,
можно воспользоваться теоремой Штейнера, которую иллюстрирует рис. 8.2. В соответствии с рис. 8.2, теорему Штейнера запишем следующей форму-
 лой:
лой:
 |

 где I0 – момент инерции относительно оси OО; I – момент инерции относительно оси O О; а – расстояние между осями.
где I0 – момент инерции относительно оси OО; I – момент инерции относительно оси O О; а – расстояние между осями.
, (8.12)
 '
'
'
|
 m
m  a
a  I
I
Рис. 8.4
Ниже приведем моменты инерции I0 для некоторых тел.
Обруч
I0 mR 2, где R – радиус обруча. (8.13

 I 0
I 0
 69
69
 Диск: I0
Диск: I0
, где R – радиус диска. (8.14)
Шар:
I0 mR 2, где R – радиус шара. (8.15)

 O
O
 Стержень:
Стержень:
I m l 2
 , где l – длина стержня; (8.16) m – масса рассматриваемых тел.
, где l – длина стержня; (8.16) m – масса рассматриваемых тел.
|
нему и проходящей через конец стержня оси
O  O
O 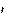 .
.
В нашем примере
I0 опре-
деляется формулой (8.16), величина a = l /2. Применяя теорему Штейнера (8.12), получим:







 1 m l 2 1
1 m l 2 1
I ma 2 m l 2 m
m l 2 m l 2 . (8.17)
0 12 4 3
В заключение отметим, что всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси подобно тому, как тело обладает массой независимо от того, движется оно или находит- ся в покое. (При вращательном движении момент инерции является мерой инертности. Момент инерции зависит от массы тела и от распределения этой массы относительно оси вращения.)
ИТОГИ ЛЕКЦИИ № 8
1. Мерой внешнего воздействия при вращательном движении твердого те-
ла вокруг закрепленной оси является момент силы Mz
относительно оси z. Мо-
дуль момента силы Mz
дает формула (8.2):
Mz =RFτ
 и иллюстрирует рис. 8.1.
и иллюстрирует рис. 8.1.
2.  Элементарная работа dA при повороте на угол d равна произведению
Элементарная работа dA при повороте на угол d равна произведению
момента силы Mz
на угол поворота d и выражается формулой (8.1):
 dA
dA 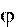 .
.
3. Момент инерции твердого тела
Iz относительно оси z является мерой
инертности при вращательном движении и по определению (8.5) равен сумме произведений масс на квадраты их расстояний до оси вращения:

|
|
4. Кинетическая энергия формуле (8.6):
Wк при вращательном движении находится по

 I
I
Wк .
2
5. Теорема Штейнера позволяет найти момент инерции I относительно
любой оси, если известен момент инерции I0
относительно оси, параллельной
данной и проходящей через центр инерции тела (8.12):


|
здесь а – расстояние между осями.
ЛЕКЦИЯ № 9
 2020-04-11
2020-04-11 669
669








