Закон сохранения момента импульса
§ 1. Уравнение динамики вращательного движения
Как отмечено в лекции № 7, § 5, для решения основной задачи механики вращательного движения тела с закрепленной осью необходимо знать зависи- мость углового ускорения 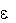 от времени. Эта зависимость находится из уравне- ния динамики вращательного движения, которое аналогично второму закону Ньютона (4.4) в динамике материальной точки. Как мы выяснили в § 1, 2 пре- дыдущей лекции мерой внешнего воздействия при вращательном движении,
от времени. Эта зависимость находится из уравне- ния динамики вращательного движения, которое аналогично второму закону Ньютона (4.4) в динамике материальной точки. Как мы выяснили в § 1, 2 пре- дыдущей лекции мерой внешнего воздействия при вращательном движении,
аналогом силы F, является момент силы Mz
относительно оси вращения Z;
аналогом массы, мерой инертности при вращательном движении, является мо-
мент инерции Iz
относительно оси Z. Роль ускорения играет угловое ускоре-
 ние. По аналогии со вторым законом Ньютона можно сконструировать из
ние. По аналогии со вторым законом Ньютона можно сконструировать из
Mz,
Iz , уравнение динамики вращательного движения:




Mz Izε.
Так как мы рассматриваем вращение вокруг закрепленной оси z, то урав- нение динамики вращательного движения записано, в отличие от второго зако- на Ньютона, не в векторном виде, а в скалярном. Можно строго доказать, что из второго закона Ньютона следует уравнение динамики вращательного движе- ния, т.е. стрелочка, связывающая две предыдущие формулы обозначает слово
«следует».
Мы получим уравнение динамики вращательного движения, опираясь на теорему о кинетической энергии. Из (5.7) и (5.8) имеем:
 dA dW К.
dA dW К.
Работу dA и приращение кинетической энергии
dWк
выразим, в соот-
ветствии с формулами (8.1) и (8.6), через величины, характеризующие враща- тельное движение:

 Mz d d I.
Mz d d I.
 Заменяя, в соответствии с (7.1а), d
Заменяя, в соответствии с (7.1а), d
вание в правой части, получим:
dt и выполняя дифференциро-
Откуда
Mz dt
 Mz
Mz
Iz d



 z dt
z dt
.
. (9.1)
Наконец, используя определение углового ускорения (7.2), получим ос- новное уравнение динамики вращательного движения:
|
Отметим, что формула (9.1) так же как и (9.2), является выражением урав- нения динамики вращательного движения твердого тела относительно закреп- ленной оси.
§ 2. Момент импульса
Запишем основной закон динамики вращательного движения в форме
(9.1), а затем занесем момент инерции Iz
под знак производной по времени:
или
M z Iz dt


 d (Iz
d (Iz
Mz dt
,
)
. (9.3)
Формула (9.3) эквивалентна формуле (9.1) при постоянном моменте инер- ции. Более общей является формула (9.3), она справедлива и в том случае, если момент инерции тела изменяется с течением времени. Эта ситуация аналогична соотношению между двумя формами записи основного закона динамики мате- риальной точки – второго закона Ньютона – в виде (4.3а) и (4.4).
Введем понятие момента импульса
Lz абсолютно твердого тела относи-
тельно оси вращения Z следующим определением:

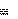 . (9.4)
. (9.4)
 Можно показать, что для однородного симметричного тела, вращающегося вокруг оси симметрии, справедлива векторная формула:
Можно показать, что для однородного симметричного тела, вращающегося вокруг оси симметрии, справедлива векторная формула:
. (9.5)
Формула (9.5) утверждает, что вектор момента импульса L направлен так же, как и вектор угловой скорости 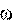 .
.
Для несимметричных тел это утверждение справедливо, если они вращают- ся вокруг одной из главных осей инерции.
С учетом (9.4) формулу (9.3) можно записать в следующем виде:

|
dt
. (9.6)
Это еще одна форма уравнения динамики вращательного движения тела вокруг неподвижной оси.
Понятие момента импульса используется не только для описания враще- ния твердых тел, но и для более общего случая движения произвольной систе-
мы материальных точек. В этом случае моментом импульса L системы ма-
териальных точек называется векторная сумма риальных точек, входящих в систему:
Li моментов импульса мате-
 N
N
L= Li. (9.7)
i=1
Момент импульса материальной точки относительно произвольной точки О пространства определяется как векторное произведение радиус-
вектора ri
материальной точки, проведенного из точки О, на вектор импульса
pi этой материальной точки (см. рис. 9.1), т.е.:
 L
L

 . (9.8)
. (9.8)
i ri pi i mi vi
На рис 9.1. материальная точка массы m движется по окружности радиуса r. Начало координат выбрано в центре этой окружности, поэтому радиус-
 L вектор r материальной точки начинается в цен- тре окружности, по которой движется точка.
L вектор r материальной точки начинается в цен- тре окружности, по которой движется точка.

 r В этом случае векторное произведение r p
r В этом случае векторное произведение r p
m v L
и, следовательно, момент импульса направле-
Рис. 9.1
ны перпендикулярно плоскости окружности, по которой движется точка.

 Опираясь на второй закон Ньютона в форме (4.3), можно показать, что закон изменения со временем момента импульса L системы имеет следующий вид:
Опираясь на второй закон Ньютона в форме (4.3), можно показать, что закон изменения со временем момента импульса L системы имеет следующий вид:
, (9.9)
здесь M – суммарный момент внешних сил.
При сделанных выше оговорках относительно осей вращения, закон изме- нения момента импульса (9.9) применим и для описания вращения твердых тел.
§ 3. Закон сохранения момента импульса
По (9.9) производная от момента импульса по времени равна суммарному моменту внешних сил:

|
 M
M
dt
Если суммарный момент внешних сил M = 0, то:
следовательно,
dL 0,

 dt
dt
 L const.
L const.
Мы получили закон сохранения момента импульса, который формулиру- ется так: момент импульса системы материальных точек остается постоян- ным, если суммарный момент внешних сил равен нулю.
 Закон сохранения момента импульса можно применить к вращающемуся телу.
Закон сохранения момента импульса можно применить к вращающемуся телу.
Так как L
const,
то величина
Iz 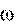 будет иметь одинаковые значения
будет иметь одинаковые значения
для любых интересующих нас моментов времени, т.е.:


 Iz Iz
Iz Iz


или
 Iz1 1
Iz1 1
 Iz2 2.
Iz2 2.
Вращающееся тело может изменить свой момент инерции, изменится и его угловая скорость, но при равенстве нулю суммарного момента внешних сил ве-
личина
Iz 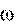 останется постоянной.
останется постоянной.
Пример – фигурист в «волчке», схематически изображенный на рис. 9.1, иллюстрирует применение закона сохранения момента импульса.


 Фигурист, раскинув руки в стороны, отталкивается ногой ото льда и начи- нает вращаться с угловой скоростью 1. При этом его момент инерции I1 за счет отведенной в сторону ноги и раскинутых рук велик. Затем фигурист при- жимает к туловищу руки и сводит вместе ноги, уменьшая их расстояние до оси вращения. Поэтому его момент инерции I2 становится заметно меньше, чем I1. Так как трение об лед невелико, то можно считать, что момент импульса I ос-
Фигурист, раскинув руки в стороны, отталкивается ногой ото льда и начи- нает вращаться с угловой скоростью 1. При этом его момент инерции I1 за счет отведенной в сторону ноги и раскинутых рук велик. Затем фигурист при- жимает к туловищу руки и сводит вместе ноги, уменьшая их расстояние до оси вращения. Поэтому его момент инерции I2 становится заметно меньше, чем I1. Так как трение об лед невелико, то можно считать, что момент импульса I ос-
 тается постоянным, поэтому угловая скорость фигуриста 2 становится замет- но больше, чем
тается постоянным, поэтому угловая скорость фигуриста 2 становится замет- но больше, чем
 Аналогичные приемы используют балерины, выполняя фуэте, акробаты и гимнасты, делая сальто. Во всех этих случаях работает закон сохранения мо- мента импульса.
Аналогичные приемы используют балерины, выполняя фуэте, акробаты и гимнасты, делая сальто. Во всех этих случаях работает закон сохранения мо- мента импульса.
 |
 I2
I2
 |


|
 Iz1
Iz1
 z2 ,
z2 ,
2


|
Рис. 9.2
§ 4. Гироскопы
Гироскопом называется быстро вращающееся массивное симметричное тело, ось вращения которого (его ось симметрии) может изменять свое на- правление в пространстве.
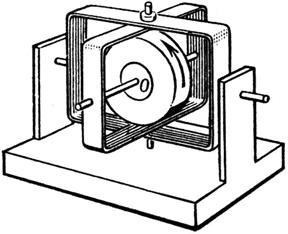
Рис. 9.3 76
У гироскопов, применяемых в технике, свободный поворот оси ги- роскопа обеспечивают, закрепляя ги- роскопы в рамках (кольцах) кардано- ва подвеса (рис. 9.3).
Такой гироскоп имеет три степе- ни свободы: он может совершать не- зависимые повороты вокруг трех осей, пересекающихся в центре под- веса О.
Если центр тяжести гироскопа совпадает с центром подвеса О, то момент сил тяжести, действующих на гироскоп, будет равен нулю.
Трение в подшипниках всех трех осей стараются сделать как можно мень- ше, таким, чтобы моментом сил трения можно было пренебречь. С учетом это-
го, момент внешних сил M относительно центра гироскопа можно считать равным нулю. Как было показано в § 3 на основе формулы (9.9), при этом усло-
вии момент импульса гироскопа L не изменяется с течением времени. Для симметричного тела, вращающегося вокруг оси симметрии, момент импульса, в
 соответствии с (9.5), равен:
соответствии с (9.5), равен:
L I .
 Таким образом, направление вектора угловой скорости гироскопа оста- ется неизменным с течением времени.
Таким образом, направление вектора угловой скорости гироскопа оста- ется неизменным с течением времени.
Это значит, что ось гироскопа сохраняет свое направление в мировом про- странстве неизменным. Если эта ось при раскрутке гироскопа была направлена на какую-нибудь звезду, то при любых перемещениях гироскопа она будет про- должать указывать на эту звезду.
Удивительным, с точки зрения житейского здравого смысла, является по- ведение гироскопа при действии на него момента внешних сил.
Пусть, как это изображено на рис. 9.4, ось гироскопа закреплена в точке О.
 Сила тяжести F казалось бы, должна поворачивать гироскоп вниз, во-
Сила тяжести F казалось бы, должна поворачивать гироскоп вниз, во-
круг оси y. Опыт же показывает, что гироскоп будет двигаться не по направле-
нию силы
mg, а перпендикулярно ей! Он будет вращаться относительно оси z
в сторону оси y.
Этот результат согласуется с предсказанием закона изменения момента импульса (9.9):
 dL
dL
 M.
M.
dt
В самом деле, момент силы тяжести относительно точки О, в соответствии с формулой (8.4), направлен по правилу правого винта вдоль оси y:

|
 r
r 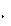 mg
mg  .
.
Бесконечно малое приращение момента импульса (9.9), будет направлено туда же:
dL,
в соответствии с

 dL M dt. (9.10)
dL M dt. (9.10)
На рис. 9.4 вектор начального момента импульса Lo
изображен исходя-



 щим из точки О. Вектор L, изображающий момент импульса через промежуток времени dt, будет повернут относительно оси z в направлении оси y, так как (рис. 9.4):
щим из точки О. Вектор L, изображающий момент импульса через промежуток времени dt, будет повернут относительно оси z в направлении оси y, так как (рис. 9.4):
 L Lo
L Lo
dL Lo
M dt.

Рис. 9.4
 Это парадоксальное, на первый взгляд, предсказание закона изменения момента импульса, как было уже сказано выше, согласуется с реальным пове- дением гироскопа. Такое движение гироскопа называется регулярной прецессией.
Это парадоксальное, на первый взгляд, предсказание закона изменения момента импульса, как было уже сказано выше, согласуется с реальным пове- дением гироскопа. Такое движение гироскопа называется регулярной прецессией.
Найдем угловую скорость прецессии пр. В соответствии с определением (7.1):

 . (9.11)
. (9.11)
 Из рис. 9.4. радианная мера угла d будет равна:
Из рис. 9.4. радианная мера угла d будет равна:
Из (9.10) и (9.12) следует, что
Из (9.11) и (9.13) получим:
d . (9.12)

 d . (9.13)
d . (9.13)


 M
M
. (9.14)

 Lo
Lo
Подставляя Lo
, где
- скорость вращения гироскопа, получим:

 (9.15)
(9.15)
Формула (9.15) замечательна тем, что в соответствии с ней угловая ско-
 рость прецессии будет постоянной при действии на гироскоп момента
рость прецессии будет постоянной при действии на гироскоп момента
 внешней силы. При исчезновении этого момента также обращается в ноль.
внешней силы. При исчезновении этого момента также обращается в ноль.
 Из (9.15) следует, что чем больше момент импульса гироскопа I
Из (9.15) следует, что чем больше момент импульса гироскопа I
o, тем
 меньше скорость прецессии.
меньше скорость прецессии.
 Отметим, что формула (9.15) справедлива при условии, что угловая ско- рость вращения гироскопа намного больше, чем скорость прецессии, т.е., если
Отметим, что формула (9.15) справедлива при условии, что угловая ско- рость вращения гироскопа намного больше, чем скорость прецессии, т.е., если
.
В заключение скажем, что в настоящее время разработаны и используются гироскопы, работающие на других физических принципах. Это волоконно- оптические гироскопы, лазерные гироскопы, ядерные гироскопы.
ИТОГИ ИЗ ЛЕКЦИИ № 9
1. Основное уравнение динамики вращательного движения твердого тела относительно закрепленной оси имеет следующий вид (9.2):
 Mz Iz
Mz Iz 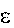 .
.
2.  Моментом импульса Lz
Моментом импульса Lz
абсолютно твердого тела относительно оси z
(9.4) называется произведение момента инерции
Iz на угловую скорость

 Lz Iz
Lz Iz
3. Основное уравнение динамики вращательного движения можно запи-
сать в виде (9.6):
 Mz .
Mz .
4. Момент импульса материальной точки mi
относительно произвольной
точки О пространства равен векторному произведению радиус-вектора r на импульс p (9.8):


 L
L
i i pi
ri mi vi.
5. Момент импульса системы материальных точек L равен векторной сумме моментов импульса материальных точек, входящих в систему (9.7):

L=
i=1
6. Закон изменения момента импульса системы со временем имеет сле-
дующий вид (9.9):

M ,
dt
здесь M – суммарный момент внешних сил.
7. Закон сохранения момента импульса гласит: момент импульса системы материальных точек остается постоянным, если суммарный момент внешних
сил равен нулю.
8. Гироскопом называется быстро вращающееся массивное симметричное тело, ось вращения которого (его ось симметрии) может изменять свое направ-
ление в пространстве.
9. Если центр тяжести гироскопа совпадает с центром подвеса, то ось ги- роскопа сохраняет свое направление в пространстве неизменным.
10. При действии на гироскоп момента внешних сил он совершает прецес-

 сию (см. рис. 9.4) со скоростью определяемой формулой (9.15):
сию (см. рис. 9.4) со скоростью определяемой формулой (9.15):
 ,
,


где M – модуль момента внешних сил, действующих на гироскоп;
 I – момент инерции гироскопа;
I – момент инерции гироскопа;
– угловая скорость его вращения.
 2020-04-11
2020-04-11 245
245








