Рассмотрим исходную систему линейных уравнений и эквивалентную ей приведенную систему (1):
| a11x1+a12x2+…+a1nxn = b1 a21x1+a22x2+…+a2nxn = b2 … am1x1+am2x2+…+amnxn = bm | x1 = a11×x1+a12×x2+...+a1n×xn + β1 x2 = a21×x1+a22×x2+...+a2n×xn + β2 ... xn = an1×x1+an2×x2+...+ann×xn + β1 |
При решении системы (1) методом простой итерации каждый шаг итерационного процесса состоит в переходе от уже имеющегося приближения значений неизвестных x(k-1) к новому (очередному) приближению x(k). Обозначим элементы имеющегося приближения через x1, x2, …, xn, а элементы очередного (вычисляемого) приближения через y1, y2, …, yn. Тогда вычислительные формулы имеют вид:
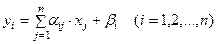
Основная идея метода Зейделя состоит в том, что на каждом шаге итерационного процесса при вычислении yi учитываются уже полученные значения y1, y2,.., yi-1. Соответственно вычислительные формулы примут вид:
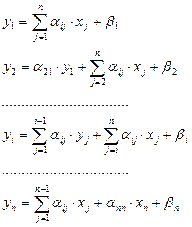
Если для матрицы коэффициентов системы (1) выполняется хотя бы одно из условий сходимости (a, b, c), то итерационный процесс сходится к единственному решению системы при любом выборе начального приближения x1, x2, …, xn.
Замечание. Преимущество метода Зейделя состоит в том, что он обычно обеспечивает более быструю сходимость, чем метод простой итерации.
Так как «вручную» осуществлять переход от исходной системы к системе (1) неудобно, опишем практическую схему преобразования исходной системы, гарантирующую сходимость итерационного процесса метода Зейделя для системы (1).
Запишем начальную систему в матричной форме:A ∙ X = B.
Умножим левую и правую части равенства на AT: AT ∙ A ∙ X = AT ∙ B. Пусть C = AT ∙ A и D = AT ∙ B. Преобразованная система имеет вид: C ∙ X = D. Такая система называется «нормальной» и обладает следующими свойствами:
1) матрица С является симметрической (т.е. cij = cji);
2) все элементы главной диагонали матрицы С нормальной системы положительны (cij >0).
Последнее свойство позволяет привести нормальную систему к виду:

Теорема. (без доказательства). Итерационный процесс Зейделя для системы (*), эквивалентный системе (1), всегда сходится к единственному решению этой системы при любом начальном приближении.
Пример. Система уравнений имеет вид:
| x1 +x2+x3 = 3 2x1 +x2+x3 = 4 x1 + 3x2 +x3 = 5 | 
| 
| 
|
Вычислим: 
Нормальная система имеет вид:
| 6x1 +6x2+4x3 = 16 6x1 +11x2+5x3 = 22 4x1 + 5x2 +3x3 = 12 | x1 = -x2 – 0,67x3 + 2,67 x2 = -0,55x1 – 0,45x3 +2 x3 = -1,33x1 –1,67x2 + 4 |
| Расчетные формулы итерационного процесса метода Зейделя для данного случая имеют вид:
| |
| y1 = -x2 – 0,67x3 + 2,67 y2 = -0,55y1 – 0,45x3 +2 y3 = -1,33y1 –1,67y2 + 4 | Окончанием итерационного процесса будем считать момент, когда для всех пар (xi, yi) в двух последовательных приближениях будет выполняться соотношение: | xi - yi | < ε |
 2020-04-12
2020-04-12 180
180








