2020-04-12
169
Пусть функция f задана табличными значениями. Построим интерполяционный полином Ln(x), степень которого не больше n и для которого выполнены условия (2):
Ln(x) = l0(x) + l1(x) + … + ln(x) (5)
Где li(x) - полином степени n, причем 
Таким образом, требование (6) с учетом (5) полностью обеспечивает выполнение условия (2).
Представим полиномы li(x) следующим образом:
li(x) = ci ·(x – x0) · (x – x1) · … · (x - xi-1) · (x – xi+1) · …· (x - xn) (7)
где ci – const, значение которой найдем из первой части условия (6): 
Итак, получим:
- интерполяционный полином Лагранжа.
Пример. Построить интерполяционный полином Лагранжа для функции, заданной таблицей:
| X | 1 | 3 | 4 |
| f(x) | 12 | 4 | 6 |
x0 = 1; x1 = 3; x2 = 4; n = 2;
y0 = 12; y1 = 4; y2 = 6.
Используя обозначение Пn+1(x) = (x – x0) · (x – x1) · …· (x - xn), получим более компактный вид интерполяционного полинома Лагранжа. Для этого продифференцируем Пn+1(x) по x:
При x = xi имеем: П’n+1(x) = (xi – x0) ·…· (xi – xi-1) (xi – xi+!) · …· (xi - xn). Тогда формула Лагранжа имеет вид: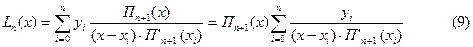 
Интерполяционные полиномы Ньютона для равноотстоящих узлов
|
|
|
Часто интерполирование ведется для функций, заданных таблицами с равноотстоящими значениями аргумента: h = xi+1 - xi (i = 0, 1, 2, …, n) – const. Для таких таблиц построение интерполяционной формулы упрощается.
Конечные разности
Пусть функция задана таблицей
| X | x0 | x1 | … | xn |
| f(x) | y0 | y1 | … | yn |
Разности между значениями функции в соседних узлах интерполяции называются конечными разностями 1-го порядка:
Dyi = yi+1 – yi (i = 0, 1, 2, …)
Из конечных разностей 1-го порядка образуются конечные разности 2-го порядка:
D2yi = Dyi+1 – Dyi (i = 0, 1, 2, …)
Продолжая этот процесс, можно по заданной таблице функции составить таблицу конечных разностей:
| x | y | Dyi | D2yi | D3yi | … |
| X0 | y0 | Dy0 | D2y0 | D3y0 | … |
| X1 | y1 | Dy1 | D2y1 | D3y1 | … |
| X2 | y2 | Dy2 | D2y2 | … | |
| X3 | y3 | Dy3 | … | ||
| X4 | y4 | … | |||
| … | … |
Конечные разности любого порядка могут быть представлены через значения функции:
Dyi = yi+1 – yi
D2yi = Dyi+1 – Dyi = (yi+2 – yi+1) – (yi+1 - yi) = yi+2 – 2yi+1 + yi
D3yi = D2yi+1 – D2yi = yi+3 – 2yi+2 + yi+1 - yi+2 – 2yi+1 + yi = yi+3 – 3yi+2 + 3yi+1 - yi
и так далее.
Методом математической индукции можно доказать, что
