2020-04-07
131
Для определения частотных характеристик периодических сигналов, т.е
для их спектрального анализа, сигналы представляются в виде суммы гармонических колебаний путем разложения в ряд Фурье. Такое разложение существует, так как большинство применяемых на практике сигналов описывается функциями времени, удовлетворяющими условиям Дирихле: наличие конечного числа разрывов первого рода (скачков) и отсутствие разрывов второго рода (ветвей, уходящих в бесконечность), а также наличие конечного числа экстремумов.
Представление периодических сигналов в виде суммы гармонических колебаний с различными параметрами (прежде всего различными частотами) называют спектральным разложением или гармоническим спектральным анализом сигналов. Математически спектральный анализ предполагает разложение сигналов в ряд по тригонометрическим функциям – синусам и косинусам. Эти функции описывают гармонические колебания, которые сохраняют свою форму в процессе преобразований линейными устройствами (изменяются только амплитуда и фаза), что позволяет использовать теорию колебательных систем для анализа свойств радиотехнических цепей. Совокупность гармонических компонент образует спектр сигнала.
|
|
|
1) Тригонометрическая форма ряда Фурье.
Тригонометрическая форма ряда Фурье имеет вид:
,
Коэффициенты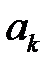 
и 
этого ряда определяются выражениями:
; 
.
Частота 
, где T – период сигнала.
Практическое применение имеет другая форма записи тригонометрического ряда Фурье:
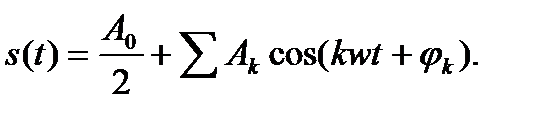
Получение такого ряда Фурье основано на известном преобразовании:
где 
и 
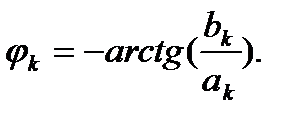
Совокупность составляющей 
и амплитуд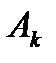 
называют амплитудным спктром,а совокупность фаз 
- фазовым спектромсигнала.
2) Комплексная форма ряда Фурье.
Комплексная форма ряда Фурье имеет вид:
Получение такого ряда Фурье основано на преобразовании тригонометрической формы ряда с использованием формул Эйлера:
; 
.
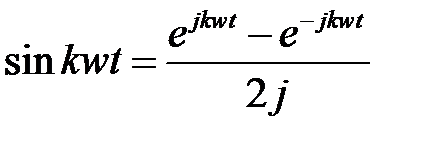Коэффициенты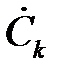 
являются комплексными амплитудами k -х гармонических составляющих, oни определяются выражением:
,
Причем 
где 
, 
.
Расчет
Графическое изображение периодической последовательности видеоимпульсов отображено на рисунке 4.
Данные для расчёта:
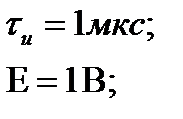
Сигнал:
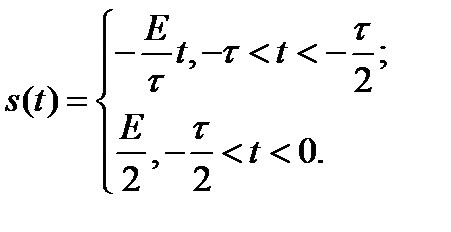
Заметив схожесть расчёта периодической последовательности видеоимпульсов и непериодического видеоимпульса можем записать:
Для построения графиков воспользуемся программой MatLab. Полученные графики спектра амплитуд и спектра фаз представлены на рисунке 5 и рисунке 6 соответственно.
