Скалярное произведение векторов в трехмерном евклидовой пространстве.
 Определение: Скалярным произведением ненулевых векторов
Определение: Скалярным произведением ненулевых векторов  и
и 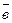 наз. число, которое равно произведению длин этих векторов, умноженное. на cos угла между векторами.
наз. число, которое равно произведению длин этих векторов, умноженное. на cos угла между векторами. 
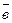 =│
=│  │*│
│*│ 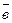 │cos(а^в) (1)
│cos(а^в) (1)
Векторное произведение тесно связано с понятием длины отрезка и величины угла.
Часный случай:  *
*  =│
=│  │*│
│*│  │cos0=│
│cos0=│  │2; │
│2; │  │2=
│2=  2 → │
2 → │  │=
│= 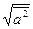 ;
;
(1) =>cosα = ( *
* 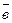 )/(│
)/(│  │*│
│*│ 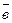 │)=(
│)=( *
* 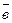 )/(
)/(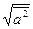 *
* 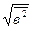 );
);
мы видим, что длину вектара и угол между векторами можна найти с помощью скалярного произведения. Все это верно и в плоскости, и в пространстве.
Свойства скалярного произведения:
1.  *
* 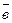 =
= 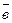 *
*  ; 2. (
; 2. ( +
+ 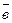 )*
)* 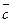 =
=  *
* 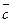 +
+ 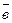 *
* 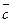 ; 3. (
; 3. (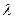 *
*  )
) 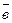 =
= 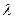 (
( *
* 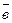 ); 4.
); 4.  *
*  =
=  2 > 0, калі
2 > 0, калі 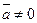
Док-во:
1.) 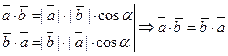
2.) Нам понадобится понятие проекцыи вектара на вектар.
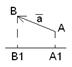
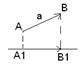 Проекцыя вектара
Проекцыя вектара  на
на 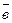 :
: 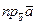
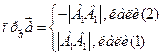 (1) (2)
(1) (2)
Между скалярным произведением и проекцыяй вектара на вектар имеет место наст. связь: 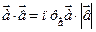
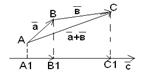 Доказ свойства 2:
Доказ свойства 2: 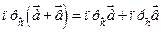
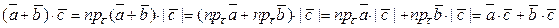
Вывод формулы для вычисления скалярного произведения векторов, заданных координатами. Для того, чтобы найти скалярное произведение двух векторов и, разложенных по базисных векторах, надо скалярного перемножить эти две линейные комбинации. Для этого нужно знать скалярные достижения базисных векторов, поэтому при вычислении скалярного произведения обычно пользуются артавнармаваным векторным базисом (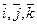 ).
).
Пускай вектар  =x1
=x1 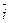 +y1
+y1 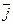 +z1
+z1 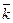 ;
; 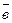 = x2
= x2 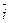 +y2
+y2 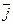 +z2
+z2 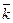 ;
;
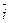 2=│
2=│ 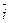 │2=1,
│2=1, 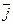 2=
2= 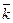 2=1,
2=1, 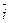 *
* 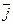 =
= 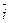 *
* 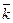 =
= 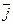 *
* 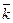 = 0.
= 0.
По-этому  *
* 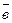 = x1 x2+ y1 y2+ z1 z2 .
= x1 x2+ y1 y2+ z1 z2 .
Практическое использование сколярного произведения вектаров.
Задача. Найти расстояние от пункта А (x1,y1,z1) до В (x2, y2, z2) заданных в декартовой системе координат.
Решение:
│АВ│=│ 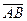 │=
│= 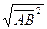 ;
;
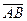 =(x2- x1; y2- y1; z2- z1);
=(x2- x1; y2- y1; z2- z1);
│АВ│= 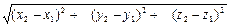
Когда пункты А и В находятся в координатной плоскасти Оху, тогда z1=z2=0; │АВ│= 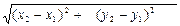
Векторное произведение векторов в трехмерном евклидовом пространстве.
Опред. Векторное пространство V вместе со скалярным произведением на нём наз. Евклидовым векторным пространством. Е = V + скал. произведением.
Опред: Скалярным произведением ненулевых векторов  и
и 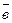 наз. число, которое равно произведению длин этих векторов, умноженное. на cos угла между векторами.
наз. число, которое равно произведению длин этих векторов, умноженное. на cos угла между векторами. 
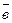 =│
=│  │*│
│*│ 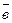 │cos(а^в) (1)
│cos(а^в) (1)
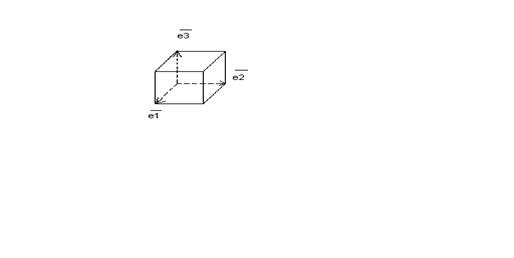
[Пуская 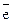 1,
1,  2,
2,  3 базис вектаров пространства.
3 базис вектаров пространства. 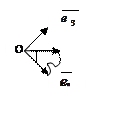
Вектар  1, можна повернуць вокруг точки О в плоскасті α так, чтобы его направление превратилось в направление вектара
1, можна повернуць вокруг точки О в плоскасті α так, чтобы его направление превратилось в направление вектара  2. Для такого поворота 2 возможности. Базис
2. Для такого поворота 2 возможности. Базис  1,
1,  2,
2,  3 наз-ся правым, если такой поворот с конца вектора
3 наз-ся правым, если такой поворот с конца вектора  3 выглядит поворотом против часовой стрелки. Все другие базисе называются левыми. Кали в Базис змяниць месцами два вектора, то права зробицца левым, а левый - правым.]
3 выглядит поворотом против часовой стрелки. Все другие базисе называются левыми. Кали в Базис змяниць месцами два вектора, то права зробицца левым, а левый - правым.]
Примеры евклидового вектарного пространства:
1) 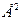 - геометрические веткоры плоскати
- геометрические веткоры плоскати
2) 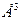 - геометрические векторы пространства
- геометрические векторы пространства
3) 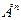 - геом. вект. пространства сторон длины n
- геом. вект. пространства сторон длины n
 Опр. Векторным произведением геометричеких векторов в пространстве
Опр. Векторным произведением геометричеких векторов в пространстве 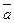 і
і  наз. вектар
наз. вектар 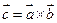 , который удовлетворяет следующим условия: 1.
, который удовлетворяет следующим условия: 1. 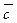 ⊥
⊥  ,
, 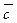 ⊥
⊥  . 2. │
. 2. │ 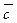 │=│
│=│  │*│
│*│  │*sinα. 3.
│*sinα. 3.  ,
,  ,
, 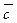 -образуют правый базис, когда
-образуют правый базис, когда  і
і  - не колинеарны (угол или ноль, или 180˚) (и sinα=0
- не колинеарны (угол или ноль, или 180˚) (и sinα=0 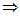 │
│ 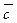 │=0 =>
│=0 => 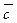 =
= 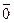 =>
=>
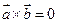 . Когда колинеарны, то это
. Когда колинеарны, то это 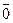 )
)
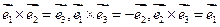
Всё это верно для каждого правого ортаунармаванага базіса.
(Базис 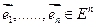 наз. ортаунармаваным, когда скалярное произведение вект.
наз. ортаунармаваным, когда скалярное произведение вект. 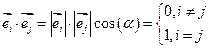 )
)
Свойства векторного произведения векторов;
1. [ 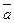 х
х  ]=
]= 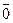 <=>
<=> 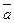 ∥
∥  . Док-во: Если хотя бы один из векторов
. Док-во: Если хотя бы один из векторов 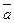 і
і  нулевой, то
нулевой, то 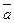 ∥
∥  и это совйство выполняется. Имеет место и обратное: пускай
и это совйство выполняется. Имеет место и обратное: пускай  <>
<> 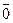 ,
,  <>
<> 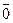 , тогда [
, тогда [ 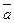 х
х  ]=
]= 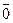 <=> │[
<=> │[ 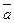 х
х  ]│=
]│= 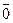 <=>
<=> 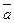 ∥
∥  .
.
2. 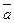 х
х  =-
=-  х
х  .
.
3. (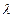
 )х
)х  =
= 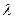 (
( х
х  );
);  х (
х (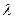
 )=
)= 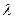 (
( х
х  ).
).
4. ( 1+
1+  2) х
2) х  =
=  1х
1х  +
+  2х
2х  ;
;  х (
х ( 1+
1+  2)=
2)=  х
х  1+
1+  х
х 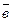 2.
2.
Вывод формулы векторного произведения векторов, заданных координатами. Выведем вычисление форм. вект. Произв. векторов  і
і  заданных своими разложения в ортавнармаваным базисе
заданных своими разложения в ортавнармаваным базисе  1,
1,  2,
2,  3.
3.
Теорема: Пускай в правым ортавнармаваным базисе  1,
1,  2,
2,  3.:
3.:  (а1,а2, а3),
(а1,а2, а3),  (b1,b2, b3), тады
(b1,b2, b3), тады 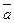 х
х  =
= 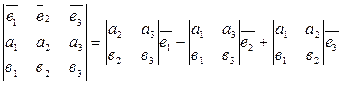
Док-во  х
х  =(а1
=(а1  1+а2
1+а2  2+а3
2+а3  3) х (в1
3) х (в1  1+в2
1+в2  2+в3
2+в3  3)= а1 в2
3)= а1 в2  1*
1*  2+ а1 в3
2+ а1 в3  1*
1*  3+ а2 в1
3+ а2 в1  2*
2*  1+ а2 в3
1+ а2 в3  2*
2*  3+ а3 в1
3+ а3 в1  3*
3*  1+ а3 в2
1+ а3 в2  3*
3*  2= а1 в2
2= а1 в2  3- а1 в3
3- а1 в3  2- а2 в1
2- а2 в1  3+ а2 в3
3+ а2 в3  1+ а3 в1
1+ а3 в1  2- а3в2
2- а3в2  1=
1=  1(а2 в3- а3 в2)-(а1 в3- а3 в1)
1(а2 в3- а3 в2)-(а1 в3- а3 в1)  2+(а1 в2- а2 в1)
2+(а1 в2- а2 в1)  3=
3= 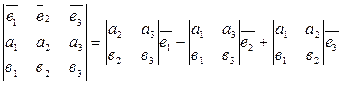 .
.
Геометрический смысл длины векторного произведения. | 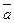 х
х  |=SABCD, когда векторы некалиниарны (не лежат в одной плоскости). ABCD – параллелограмм.
|=SABCD, когда векторы некалиниарны (не лежат в одной плоскости). ABCD – параллелограмм.
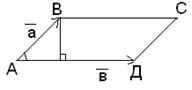
Док-во: 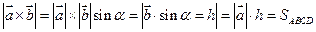
(эти сведения нужны для практического применения вект. пр.)
Практическое использование векторного произведения векторов. Задача. Найти Sтрох-ка АВС, когда А(x1;y1;z1), B(x2;y2;z2), C(x3;y3;z3).
 2020-04-12
2020-04-12 468
468







