Паралелограмм: Изображением данногог паралелограмма м.б. произвольный пар-м

Используем паралельнасть прямых.

 

4. Трапецыя: изображение данной трапецыі м.б. произвольнгая трапецыя с тем же отношением оснований асноў. Т.як // прямых сохраняется, то трапецыя перех. у трапецыю.  Док-но, что изображение данной трапецыі м.б. произвольнгая трапецыя с тем же отношением оснований асноў.

5. окружнасть: Рассм поняцие афин. отображение. Пл-и на плоскасть. П, П¹.    

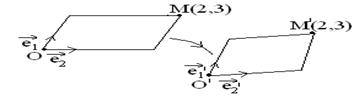
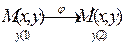
При афин. преобразовании. пл-ти элипс всегда переходит в элипс. Для афин. отображения всё то же самое: эліпс переходит в элипс. Покажем, что парал. проектирование пл-ти на плоскасть есть афин. преобразование. Отсюда будет следовать, что изображения окр-ти явл. элипс. Очевидно, что наша паралл. проектирование есть афин. преобразование, которое задается реперами  изображений перпенди-ых диаметров окр-ти явл. сопряженные диаметры эллипса. Ранее было доказано, что эллипс однозначно определяется своими сопряженными диаметрами.

6. Изображение правильного шестиугольника строится на основе задачи с правильным треугольником.

Задача: Построить изображение правильного тр-ка, вписанного в окр-ть.

 

 

10. Изображения пространственных фигур в параллельной проекции.

Изображение фигуры - это ее проекция с точностью до падобнасци.Тэарэма Польке-Шварца: изображение данного тетраэдра м.б. произвольный плоский четырехугольник вместе с его диагоналями.

 

Куб. Выделим вспомогательный тетраэдра. Применим теорему Полли-Шварца, потом дастрайваем.

Полученный изображение - правильный, но не нагляден. Мы никогда не видим куб в таком виде.

При прямоугольном и проектировании праектавальныя прямые перпенди-ны плоскости проекции, при касавугольным нет. Полученный изображение куба получает. при касавугольнай проекции.

Параллелепипед. Для него верно все, что говорилось о кубе. Если паралл-д прямой, то боковые грани  лучше рисовать вертикально.

Призма. Рассмотрим вспомогательный тетраэдра. Применим теорему Полли-Шварца.

Потом, пользуясь теоремой (если при паралл. Проект. Известен изображения 3-х пунктов общего положения плоскости, то можно построить изображение произвольного пункта плоскости) строим изображение нижней основы призмы.

После этого остается испол-во паралл-во прямых.

Цылиндр.  А₀В₀, А₀С₀ - сопряженные диаметры элипса.Згодна теоремами. Поль-Шварца А₀В₀С₀D₀ есть изображение тетраэдра ABCD в некото. паралл-ой проекции.

При этом, изображением нижней основы оригинала будет некий эллипс со сполоч-ми диамате-ми А₀В₀, А₀С₀. Так как эллипс однозначно определяется своими спал-ми диамате-ми, то это изображение совпадает с основой изображения.

Шар. При параллельном проектировании шара всегда рассматривать. случай, когда это проектирование прямоугольное. При этом контур шара получает. в виде окружности. Ось шара - это диаметр шара плоскости сечения.

11.Сістэма аксіём Вейля трохмернай эўклідавай прасторы і яе несупярэчлівасць.

Осн. абъекты - действ. числа, векторы, точки.

Осн. отношения – сложение векторов, умножение вектора на число, скалярное произведение.(Скалярным произведением ненулевых вектаров и  наз. число, которое равно произведению длин этих вектаров, умножен. на cos угла между векторами. =│ │*│ │cos(а^в)), откладывание вектора от точки.

Аксиоматика Вейля содержит 15 аксиом. Все аксиомы образуют 5 груп аксиом: 4 аксиомы сложения вект., 4 акс. умнож. вект. на число, 2 акс. размерности, 3 акс. скалярного произведения, 2 акс. отклад. вектора от точки. V -векторы, E - точки.

I гр. (4 акс.) - аксиомы сложения вектаров.

1.

2.

3.

4.

II гр. (4 акс.) - акс. умнож. вект. на число.

   5.

   6.

   7.  

   8.

Мн-во V з операциями и есть вект. пр-во.

III гр. ( 2 акс.)- аксиомы размерности.

   9.  

  10.

V - 3-х мерная вектарное прастранство.

IV гр. ( 3 акс.)- акс. скалярного произведения.

  11.

  12.  13.

      

           

 

- неравенство Коши-Буняковского. Док-тся, что существ. базис , такой что длинна каждого вектора еденица     

 

V - 3-х мерная вектарное прастранство.

V гр. ( 2 акс.)- акс. отклад. вектора от точки.

  

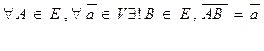
 14.

 

15.

Мн-во точек Е наз. 3-х мерным вектарным прастранством.

Первый вопрос, который возникает при работе с сист. аксиом - это вопрос о её непротиворечивости (пусть существ. сист. аксиом – А1, А2,.., Аn. это сист. аксиом наз противоречивой, когда с её помощью можно док-ть 2 теоремы, которые противоречат одна другой). Для сист. акс. Евклида этот вопрос встает только после аналог. Вопроса для геометрии Лобачевского. Клейн доказал, что геом. Лобач. Непротивор., когда непротивор. геом. Евклида.

Один из способов док-ва непротив-ти следующая. Выбир некоторая матем-я теория, напр., теория действ. чисел, с всеми осн абъектами и осн атношениям придается некоторый арифм. смысл. При этом должно быть, так чтобы все аксиомы при этом были справедливыми арифм. утвер-ми. Когда всё это получ-сь, то м. утв-ць, что наша сист. акс. непротивор, когда непритивор-ва теорыя действ. чисел.