Опред. Преобразование пл-ти наз преобразование подобия, когда все расстояния между точками изменяются в к раз. к -константа>0 (коэфицент подобия). 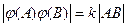
Опред. Преобразование плоскости называется преобразование подобия, когда оно является аффинным преобраз. и все расстояния между пунктами меняет в к-раз.
Опред. Гомотетией наз.каждое движение – преобразован пад-сці з к =1.
Утв.: Каждая гомотетыия з коэф. 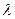 - есть падобнасць з коэфіц. к=│
- есть падобнасць з коэфіц. к=│ 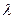 │ хˈ=
│ хˈ= 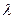 х
х
уˈ= 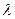 у – формулы афинного преобразования.
у – формулы афинного преобразования.
Суть метода гомотетии – для данной или искомой фигуры существует центр гаматэтыи, который задан или м. найти. Выполнив гаматэт. преобраз., получим новыя эл-ты, - связанные с искомой или данной фигурой, которые и позво-во выполнять неабход.построения.
Гомот. з центрам О і коэф. k наз. такое преобоазование, которое "п. А ставит в соответсвие. п. А', что
1. ОА'= │ k │ ОА; 2.п. О, А, А' принадл адной прамой; 3.когда k >0, п. А' лежит на луче ОА, а когда k <0, то А' лежит на луче, который дополняет ОА.
Свойсвта:
1) При гаомотетии прямая перех в прямую (т.е. гомотетия является схожестью, а каждая похожесть - афиннае первотворения, то гаматэтыя - афинное преобразования).
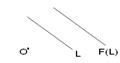 2) Каждая прямая, которая прох через центр гам-и, перех сама в себя.
2) Каждая прямая, которая прох через центр гам-и, перех сама в себя.
3) Каждая прямая переходит в параллельную ей прямую.
Док-во:
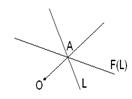
Пускай это не так и прямыя не парал-ныя, тогда они перес-тя в точке. 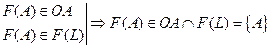
Пускай 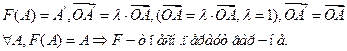
4) Гаматэтыя адназначна вызначаецца сваим цэнтрам и парай пунктау. F: О, А, А’.
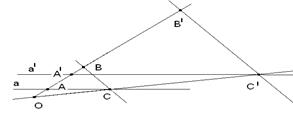
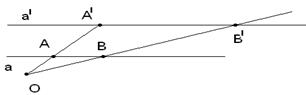
Задача:задана гаматетия Н0(А)=А'. Паостроим. образ точки В.
а) точка В 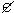 ОА б) точка В
ОА б) точка В 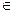 ОА
ОА
Утв1. Когда 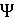 - преобразование пад-ці с коэф. к, то
- преобразование пад-ці с коэф. к, то 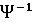 - преобразованием пад-ци с коэф. 1/к. Замечание: Т.к.
- преобразованием пад-ци с коэф. 1/к. Замечание: Т.к. 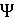 - аф.пер-не, то
- аф.пер-не, то 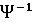 - аф.пер-не
- аф.пер-не
Утв2. Когда 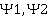 - преобразование пад-ци с коэф. к1 і к2, то композицыя
- преобразование пад-ци с коэф. к1 і к2, то композицыя 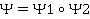 - тоже преобразование пад-ці з к = к1*к2
- тоже преобразование пад-ці з к = к1*к2
Т1. Мн-ва всех аф. Преобразований утварае группу преобразований пл-ти. Д-во: следует из утв1, утв2.
5. Группа афинных преобразований пл-ти и некоторые ее подгруппы
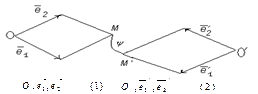
Поставим в соответствие каждому. п. пл-ти M (x, y) п. M '(x, y). Получаем пераутвар. данной пл-ти. - Афиннае пераутв., которое задается реперами (1), (2). 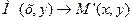 .
.
Легко видеть, что кожн. аф. пераутв. взаемооднозначно. в этом случае 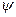 имеет отвар. пераутв.
имеет отвар. пераутв. 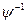 , которое задаётся реперамі
, которое задаётся реперамі 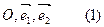 і
і 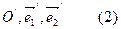 .
.
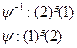
Проверим, что при этом пераводит равные векторы в равные – 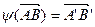 .
.

 у (1)
у (1) 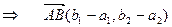 у (1)
у (1)
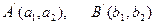 у (2)
у (2) 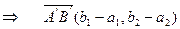 у (2). Отсюда следует, что равные. векторы переходят в равные векторы, и наше определение корректно.
у (2). Отсюда следует, что равные. векторы переходят в равные векторы, и наше определение корректно.
Т.Ч. аф. пер. дзейств. не только на пункты, но и на вектары пл-ти.
 Т: Пусть А, В, С и А ', В', С '- две тройки пунктау пл-ти общего положения. Существует ровно одно Афин. пераутвар., Такое, что
Т: Пусть А, В, С и А ', В', С '- две тройки пунктау пл-ти общего положения. Существует ровно одно Афин. пераутвар., Такое, что 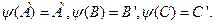
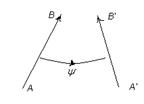 Т: (без д-ва): Аф. пер.
Т: (без д-ва): Аф. пер. 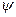 каждый рэпер пераутв. в рэпер и задается парой таких рэперав.
каждый рэпер пераутв. в рэпер и задается парой таких рэперав.
Т: Мн-ва всех аф. пер. пл-ти образует группу пераутв. пл-ти.
Д-з: 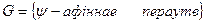 . Н-й
. Н-й 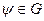
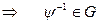 верна
верна
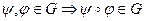 ,
, 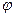 - аф. пер.
- аф. пер. 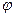 : (1),(2)
: (1),(2)
Подействуем на 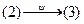 ,
, 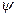 : (2), (3)
: (2), (3)
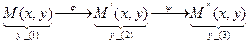 . Вид-но, что композиция
. Вид-но, что композиция 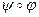 - аф. пер., задаётся (1) і (3).
- аф. пер., задаётся (1) і (3).
осн. факты аф. пер.:
1) Прямая переход. в прямую - 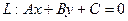 у (1),
у (1), 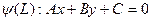 у (2).
у (2).
2) //-я пр. у //-я пр.
3) Сохраняется простое отношение 3 т.(АВС)
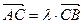 ,
, 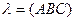
Д-во: 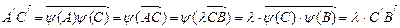
4) Отрезок в отрезок
5) Серед. отр. в сер. отр.
6) ∆ в ∆ - кажд 2 ∆-ка афинна-кангруэнтны (Две фигуры будем наз. афинна-кангурэнтными ф-ми, если одна из них переводится в другую некоторым аф. первотворения).Параллелаграм у параллелаграм - кожн 2 параллел-ма афінна-кангруэнтны
7) Кривая 2-го порядка в кривую 2-го порядка - эллипс в эллипс, гипербола в гиперболу, парабола - в параболу
8) Аф.пер. не сохр углы, расстоян, S, но сохр. отнош пл-дей
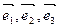 - базис вектарау пр-ва,
- базис вектарау пр-ва, 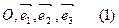 и - афинны рэпер в пр-ры, М об. п пр-ры
и - афинны рэпер в пр-ры, М об. п пр-ры 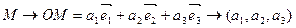
М(а1,а2,а3) – аф. координаты п.М в реперы (1), они вызн. станов. п. у пр-ве однозначно.
 2020-04-12
2020-04-12 205
205








