Пусть в простр-ве зафиксирована некот. декартава прямоуг. с/к. Пусть также π1 и π2 2 разл. плоскости, заданные общими ур-ями: А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 и  по прямой l. Т.к. пр l представлена как пересеч пл-тей π1 и π2 , то она опред сист 2 ур-ний:
по прямой l. Т.к. пр l представлена как пересеч пл-тей π1 и π2 , то она опред сист 2 ур-ний:  (1)
(1)
Очевидно, система (1) определяет пр в том случае, когда пл π1 и π2 не //-ны и не совпадают. Следовательно, система (1) определяет прямую в том, и только в том случае, когда коэфф А1, В1, С1, одного из уравн сист одновременно не пропорциональны соотв-щим коэфф А2, В2, С2 др.
Заметим, что ч/з кажд пр. проходит  много разл пл-тей. Очевидно, что сущ-ет
много разл пл-тей. Очевидно, что сущ-ет  много возможностей выбрать из них какие-нибудь две. Иными словами, всякую прямую можно определить двумя уравнениями пучка α (А1х+В1у+С1z+D1)+β(А2х+В2у+С2z+D2)= 0 (α и β - произвольно взятые не равные нулю числа)
много возможностей выбрать из них какие-нибудь две. Иными словами, всякую прямую можно определить двумя уравнениями пучка α (А1х+В1у+С1z+D1)+β(А2х+В2у+С2z+D2)= 0 (α и β - произвольно взятые не равные нулю числа)  многими способами.
многими способами.
При реш задач более удобным явл специальный вид ур прямой в пространстве.
Определение. Любой ненулевой вектор  пространства, перпендикулярный к прямой l, называется нормальным вектором прямой, а любой ненулевой вектор
пространства, перпендикулярный к прямой l, называется нормальным вектором прямой, а любой ненулевой вектор  пространства, параллельный прямой l, – направляющим вектором прямой.
пространства, параллельный прямой l, – направляющим вектором прямой.
 Выведем ур. пр. l, проходящей ч/з данную т. M1(x1, y1, z1) и имеющей заданный направляющий вектор
Выведем ур. пр. l, проходящей ч/з данную т. M1(x1, y1, z1) и имеющей заданный направляющий вектор  (l, m, n). Заметим, что произвольная точка M(x,y,z) лежит на прямой l тогда и только тогда, когда векторы
(l, m, n). Заметим, что произвольная точка M(x,y,z) лежит на прямой l тогда и только тогда, когда векторы  и
и  (a1,a2,a3) коллинеарны, (векторы, леж-ие на параллельных прямых (ілі на одной і той же прямой)) т.е при выполнении условия
(a1,a2,a3) коллинеарны, (векторы, леж-ие на параллельных прямых (ілі на одной і той же прямой)) т.е при выполнении условия  (2)
(2)
Пусть прямая задана в пространстве своими каноническими уравнениями (2). Обозначим буквой t каждое из отношений (2), которые участвуют в канонических уравнениях  =t (3)
=t (3)
Заметим, областью изменения параметра t является вся вещественная ось: -∞<t<+∞.
Проведя преобразования х-х1=a1t, у-у1 =a2t, z-z1 =a3t, окончательно получим:  (4 ) – параметрические уравнения прямой.
(4 ) – параметрические уравнения прямой.
Можно кратко записать так: 
В пространстве возм 3 случая взаимного расположения прямой и плоскости:
1) прямая принадлежит плоскости - 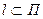 ;
;
2) прямая и плоскость пересек в точке - 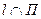 ;
;
3) прямая и плоскость не пересекаются;
Рассмотрим эти случаи:
Пусть пр. задана след. ур-ями  , пл-ть общим ур-ем
, пл-ть общим ур-ем 
Найдем общие точки L и П:

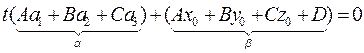
1. 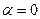 , то 2 случая
, то 2 случая
1)  , 0=0,
, 0=0, 

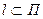 – прямая принадлежит пл-ти
– прямая принадлежит пл-ти
Если 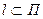 , то направляющий вектор
, то направляющий вектор 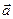 (а1, а2, а3) пр. l ортогонален нормальному вектору
(а1, а2, а3) пр. l ортогонален нормальному вектору  (А,В,С) плоскости П.
(А,В,С) плоскости П.
2)  - нет решения, т.е. прямая и плоскость не пересекаются
- нет решения, т.е. прямая и плоскость не пересекаются
2. 
 - единств. решение, т. е.
- единств. решение, т. е. 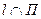 в одной т.,
в одной т., 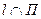 (т.е. Аа1+Ва2+Са3 ≠ 0 (5))
(т.е. Аа1+Ва2+Са3 ≠ 0 (5))
Обратно, если выполняется условие (5), то прямая l не параллельна плоскости π, а значит, пересекает ее под определенным утлом.
Частным случаем пересечения прямой и плоскости является их перпендикулярность. Прямая будет перпендикулярна плоскости в том и только в том случае, когда направляющий вектор прямой 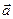 коллинеарен нормальному вектору плоскости
коллинеарен нормальному вектору плоскости  .
.
Т. обр.,  – условие перпендикулярности прямой и плоскости
– условие перпендикулярности прямой и плоскости
Утверждение: прямая параллельна плоскости - 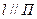

Если пр 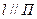 , то вып-ся только условие Аа1 + Ва2 + Са3 = 0 (6), и обратно, если вып-ся усл (6), то направляющий вектор
, то вып-ся только условие Аа1 + Ва2 + Са3 = 0 (6), и обратно, если вып-ся усл (6), то направляющий вектор 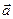 пр. ортогонален нормальному вектору
пр. ортогонален нормальному вектору 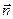 пл-ти П
пл-ти П  прямая параллельна плоскости.
прямая параллельна плоскости.
Аа1 + Ва2 + Са3 = 0 – условие параллельности прямой и плоскости.
7. Поняцие проективной плосости
В трохмерн. эвклід. пр-ве R3,  , расм. связку Р2(S) с центром у т. S - мн-ва всяких прямых і пл-тей, которые проходят через т.S.
, расм. связку Р2(S) с центром у т. S - мн-ва всяких прямых і пл-тей, которые проходят через т.S.  будзем гаварыць, что прямая а інцидентна пл-ти
будзем гаварыць, что прямая а інцидентна пл-ти  , или пл-ть
, или пл-ть  інцидентна прямой а.
інцидентна прямой а.  .
.
при центральном проектировании прямыя переходят в прямыя,или паралельнасть прямых не сохраняется, не сохраняются углы и прямая отношение 3-х точек ( ).
).
Расм. пл-ть R2, которая не праход. через центр связки S. В дальнейшем под R2 б. понимать пункты і пр. этой пл-ті.
Расм. адлюстр 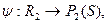 которое кажд. т. А
которое кажд. т. А  ставит в соответствие пр. связки SA, а кожн пр
ставит в соответствие пр. связки SA, а кожн пр  - пл-ть связки SA.
- пл-ть связки SA.  – перспективное переутв. пл-ті R2.
– перспективное переутв. пл-ті R2.
 Важно, что
Важно, что  сохр. Отношение инциндентности:
сохр. Отношение инциндентности: 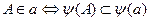 (1)
(1)
Отр.  не является взаимооднозначным, потому что пл-ть связки
не является взаимооднозначным, потому что пл-ть связки  //-ная пл-ці R2 не имеет прообраза. Не имеют прообраза и все пр. все, которые инциндентны пл-ті
//-ная пл-ці R2 не имеет прообраза. Не имеют прообраза и все пр. все, которые инциндентны пл-ті 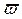 . Такие пр. зсвязки наз особыми (их
. Такие пр. зсвязки наз особыми (их  много), а пл-ть
много), а пл-ть 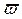 – особ. пл-тью (одна).
– особ. пл-тью (одна).
отр.  стало бы взаимно однозн, если б мы договорились, что кожн особая пр пересекает пл-ть R2 в бесконечно удаленной п., а особая пл-ть пересяк R2 на
стало бы взаимно однозн, если б мы договорились, что кожн особая пр пересекает пл-ть R2 в бесконечно удаленной п., а особая пл-ть пересяк R2 на  -ца удаленнай пр. При этом разн особые пр зсвязки адпав-ць розн
-ца удаленнай пр. При этом разн особые пр зсвязки адпав-ць розн  -ца удалённым п. R2.
-ца удалённым п. R2.
Проективная пл-ть  – пл-ть R2 вместе с присоединенными к ней няуласными эл-тамі – няуласнымі п.
– пл-ть R2 вместе с присоединенными к ней няуласными эл-тамі – няуласнымі п.  ,і няуласнай пр. а
,і няуласнай пр. а  . Пры При этом возникает взаемно однозначное растояние
. Пры При этом возникает взаемно однозначное растояние  , которое на собственные эл-ты
, которое на собственные эл-ты 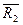 дейничае, як і
дейничае, як і  , а няуласныя эл-ты
, а няуласныя эл-ты  преводит у особ пр. і особ пл-ть
преводит у особ пр. і особ пл-ть  . Расстояние.
. Расстояние.  наз. перспективным.
наз. перспективным.
Учитывая (1), естественные требовать, каб расстояние.  тоже сохраняло отношение инциндентности:
тоже сохраняло отношение инциндентности:  (2) для собственных і не собственных эл-тау
(2) для собственных і не собственных эл-тау  . Неабходныя ул-ці эл-тау
. Неабходныя ул-ці эл-тау 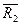 :
:
1. Каждый не собств т.  инцинд не собств пр.
инцинд не собств пр.  .
.
2. Каждый собствен. пр инцинд некоторому несобств т. и только одному.
 (на рис.
(на рис.  ,
,  - векторы)
- векторы)
Рассм связку  і у R3 аф. репер
і у R3 аф. репер  . Каждая пр.
. Каждая пр.  связки
связки  определяется главным вект
определяется главным вект  . который определяется тройкой сваих координат (x1, x2, x3) в базисе
. который определяется тройкой сваих координат (x1, x2, x3) в базисе  . В итоге
. В итоге  опред. тройка чисел (x1, x2, x3).
опред. тройка чисел (x1, x2, x3).
вместо вектара  , м.б. выбираем вект
, м.б. выбираем вект 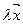 ,
,  , то тройка вызн. з точностью да лікавага множніка. (x1, x2, x3) – праект. коорд. пр.
, то тройка вызн. з точностью да лікавага множніка. (x1, x2, x3) – праект. коорд. пр.  связки
связки  . Будем писаць
. Будем писаць  .
.
Рассм праект пл-ть  ,
,  - яе персп. расстояние. Т.я.
- яе персп. расстояние. Т.я. 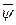 взаемнооднозначное, то калі
взаемнооднозначное, то калі  і
і  , то п.А м. прыпісаць проект коорд.
, то п.А м. прыпісаць проект коорд.  . Т.ч. на
. Т.ч. на  возникает проект. сист. коорд.
возникает проект. сист. коорд.
Т 1 (без д-ва): Е1, Е2, Е3, Е0 – произвольные. 4 т. 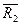 , никоторые 3 з которых не инцинд. одной пр. Тогда на
, никоторые 3 з которых не инцинд. одной пр. Тогда на 
 еденств сіст праект коорд, в которой Е1(1:0:0), Е2 (0:1:0), Е3(0:0:1), Е0 (1:1:1).
еденств сіст праект коорд, в которой Е1(1:0:0), Е2 (0:1:0), Е3(0:0:1), Е0 (1:1:1).
E1, E2, E3, E0 – проект. репер пл-ті.
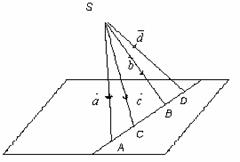 А, В, С, D – розн. п
А, В, С, D – розн. п 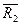 , інцинд-ные одной пр. Іх коорд-ыя слупки -
, інцинд-ные одной пр. Іх коорд-ыя слупки - 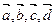 . Из рис видно, что
. Из рис видно, что  .
.
(АВСD)=  – сложн.отношение п. А, В, С, D.
– сложн.отношение п. А, В, С, D.
8. Проективное преобразование плоскасти
Проективная пл.  – пл. R2 вместе с присоединёнными да яе несобств эл-тамі – несобств п.
– пл. R2 вместе с присоединёнными да яе несобств эл-тамі – несобств п.  ,і несобств пр. а
,і несобств пр. а  . При этом возн. взаемооднозначное отн
. При этом возн. взаемооднозначное отн  , которое на собств эл-ты
, которое на собств эл-ты  дейнічеет, как і
дейнічеет, как і  , а несобств эл-ты
, а несобств эл-ты 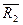 переводит в особ пр. і особ пл-ць
переводит в особ пр. і особ пл-ць  . Расст.
. Расст.  наз. перспективным.
наз. перспективным.
Считая (1), естественно потребовать, чтоб расст.  тоже сохраняло отношение инцинд:
тоже сохраняло отношение инцинд: 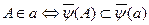 (2) для собств і несобств эл-тау
(2) для собств і несобств эл-тау  . необходимые св-ва эл-тов
. необходимые св-ва эл-тов 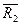 :
:
1.Каждый не собств т.  инцинд не собств пр.
инцинд не собств пр.  .
.
2.Каждый собствен. пр инцинд некоторому несобств т. и только одному.
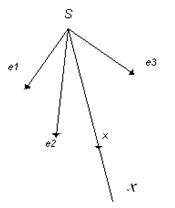 (на рис.
(на рис.  ,
,  - векторы)
- векторы)
Рассм связку  і у R3 аф. репер
і у R3 аф. репер  . Каждая пр.
. Каждая пр.  связки
связки  определяется главным вект
определяется главным вект  . который определяется тройкой сваих координат (x1, x2, x3) в базисе
. который определяется тройкой сваих координат (x1, x2, x3) в базисе  . В итоге
. В итоге  опред. тройка чисел (x1, x2, x3).
опред. тройка чисел (x1, x2, x3).
вместо вектара  , м.б. выбираем вект
, м.б. выбираем вект 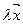 ,
,  , то тройка вызн. з точностью да лікавага множніка. (x1, x2, x3) – праект. коорд. пр.
, то тройка вызн. з точностью да лікавага множніка. (x1, x2, x3) – праект. коорд. пр.  связки
связки  . Будем писаць
. Будем писаць  .
.
Рассм праект пл-ть  ,
,  - яе персп. расстояние. Т.я.
- яе персп. расстояние. Т.я. 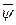 взаемнооднозначное, то калі
взаемнооднозначное, то калі  і
і  , то п.А м. прыпісаць проект коорд.
, то п.А м. прыпісаць проект коорд.  . Т.ч. на
. Т.ч. на  возникает проект. сист. коорд.
возникает проект. сист. коорд.
Т 1 (без д-ва): Е1, Е2, Е3, Е0 – произвольные. 4 т. 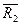 , никоторые 3 з которых не инцинд. одной пр. Тогда на
, никоторые 3 з которых не инцинд. одной пр. Тогда на 
 еденств сіст праект коорд, в которой Е1(1:0:0), Е2 (0:1:0), Е3(0:0:1), Е0 (1:1:1).
еденств сіст праект коорд, в которой Е1(1:0:0), Е2 (0:1:0), Е3(0:0:1), Е0 (1:1:1).
E1, E2, E3, E0 – проект. репер пл-ті.
 А, В, С, D – розн. п
А, В, С, D – розн. п 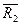 , інцинд-ные одной пр. Іх коорд-ыя слупки -
, інцинд-ные одной пр. Іх коорд-ыя слупки - 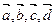 . Из рис видно, что
. Из рис видно, что  .
.
(АВСD)=  – сложн.отношение п. А, В, С, D. (АВСD)=
– сложн.отношение п. А, В, С, D. (АВСD)=  – складаная адносіна п. А, В, С, D.
– складаная адносіна п. А, В, С, D.
Проект. переутв. пл-ті  вызн. з дап. 2 проект. реперау E1, E2, E3, E0 і E1’, E2’, E3’, E0’. Пры этом
вызн. з дап. 2 проект. реперау E1, E2, E3, E0 і E1’, E2’, E3’, E0’. Пры этом 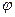 перевод. п.
перевод. п.  у п.
у п. 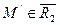 , которые в др. реперы имеет теже проект. коорд., которые имеет М в первом репперы.
, которые в др. реперы имеет теже проект. коорд., которые имеет М в первом репперы.
Т 2 (без д-ва): Каждая проект. преобр. пл-ті взаимооднозначно, прямыя переводит в прямыя и сохраняет сложные отношение 4 п. верно і адв. сцв.
Мн-во всех проект преобразований пл-ті 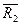 образует группу преобразований
образует группу преобразований 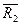 .
.
Проективная геометрия пл-ті изучает св-ва фигур 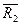 , которые сохр при всех проект. преобразованиях
, которые сохр при всех проект. преобразованиях 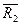 . Простое отношение 3 т. в проект геометрии не изучается, потому что она сохраняется при проект преобразовании, а сложн отнощение – изучается.
. Простое отношение 3 т. в проект геометрии не изучается, потому что она сохраняется при проект преобразовании, а сложн отнощение – изучается.
9. Св-ва паралельных проекций. Изображения плоских фигур в //-най проекциі
 При центральном проектированнии пр перех. в пр и сохр. сложн. отношение 4-х точек. Но не сохр. // пр и простое отношение 3-х точек. Это делает выполнение рисунка довольно сложным. Чтоб избежать это вместо центр. разгл. паралельнае проектированние.
При центральном проектированнии пр перех. в пр и сохр. сложн. отношение 4-х точек. Но не сохр. // пр и простое отношение 3-х точек. Это делает выполнение рисунка довольно сложным. Чтоб избежать это вместо центр. разгл. паралельнае проектированние.
В этом случае центр проекции - бесконечно дальний пункт, а праектавальныя прямые параллельные друг другу. Паралл. проектирование - частный случай центр. проектирования. При этом сохр. паралельность прямых і простае отношение 3-х точек. В школе использует именно // проект-ем. П: F  П П (М)=SM
П П (М)=SM  П=M0
П=M0
П - центральное проектаванние; SM – проективная прямая; F0 – проекция F; F – оригинал; П – плоскасть проекцый.
Изображение фигуры - это ее проекция с точностью до подобия. (Не путать изображение с проекцией!) Т.ч. проекцыя явл. частным случаем изображения.
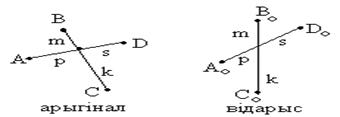 При парал. проектированнии
При парал. проектированнии 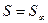 и все проект. прямыя паралельны. Прямая перех. в прямую, т.як 2 плоскасти пересек. по прямой. При парал. проект. парал-е прамые перех. в парал. прямыя, т.як 2 парал. плоскасти перес. третей парал-ой прямой.
и все проект. прямыя паралельны. Прямая перех. в прямую, т.як 2 плоскасти пересек. по прямой. При парал. проект. парал-е прамые перех. в парал. прямыя, т.як 2 парал. плоскасти перес. третей парал-ой прямой.
 Т-ма. Когда при парал. проект. известный изображения 3-х пунктов общего положения плоскости
Т-ма. Когда при парал. проект. известный изображения 3-х пунктов общего положения плоскости  , то можно построить изображение произвольного пункта плоскости
, то можно построить изображение произвольного пункта плоскости  .
.
1. Тр-к: Изображением данного  м.б. произвольный
м.б. произвольный  .
.
Доказ: Пусть АВС- данный тр-к; А0В0С0 - произвольный тр-к; А=А0, В=В0, П= А0В0С0 ; СС0 - проектав. прямая.

2. Произвольный 4-угольник: изображением данного 4-уг. м.б. произволн. 4-уг.. Используем простое отношение 3-х точек

 2020-04-12
2020-04-12 123
123








