Уравнения касательной и нормали к графику функции

1 2 3 4 5 6

Лекция

Тема: «Приложения производной»

План

Применение производной к вычислению пределов функций (правило Лопиталя).

Геометрический и механический смысл производной

Применение производной к исследованию функций и построению их графиков.

Правило Лопиталя

Правило Лопиталя применяется для нахождения предела отношения двух бесконечно малых или бесконечно больших функций, т.е. для раскрытия неопределенности вида или .

Пусть функции и определены и дифференцируемы в некоторой окрестности точки х ₀, исключая, быть может, саму точку х ₀, и пусть эти функции являются одновременно бесконечно малыми или бесконечно большими. Тогда если существует предел отношения производных при х ® х ₀, то он равен пределу отношения самих функций

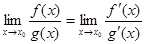Пример. Пользуясь правилом Лопиталя, найти .

Решение: Имеем неопределенность вида (0/0). Применяя правило Лопиталя, получим:

Еще смотрите здесь:

ШИПАЧЕВ В.С. Задачник по высшей математике с. 64-65 пункт 2 – выучить и рассмотреть примеры решения задач на с.65-66

Геометрический смысл производной.

Уравнения касательной и нормали к графику функции

Касательная определяется как предельное положение секущей. Прямая l называется касательной к кривой в точке M ₀, если она проходит через эту точку и угол a между прямой l и секущей MM ₀ стремится к нулю при M ® M ₀.

Производная функции f ¢(x ₀) в точке x ₀ равна угловому коэффициенту касательной к графику функции у = f (х) в точке x ₀, т. е. f ¢(x ₀) — это тангенс угла наклона касательной к оси Ox, проведенной в точке M ₀(x ₀; f (x ₀)):

f ¢(x ₀) = k _кас. = tg a.

Уравнение касательнойк графику функции y = f (x ₀) в точке M (x ₀; f (x ₀)):

y = f (х ₀) + f ¢(х ₀)(x – x ₀).

Нормалью к кривой в точке M ₀ называется прямая, проходящая через точку M ₀ перпендикулярно касательной в этой точке.

Уравнение нормали к графику функции y = f (x ₀) в точке M (x ₀; f (x ₀)):

, если f ¢(х ₀) ¹ 0,

x = x ₀, если f ¢(х ₀) = 0.

Пример. Написать уравнение касательной к графику функции y = 2 x ² + 1, параллельной прямой y = 3 – 2 x.

Решение. Касательная и прямая y = 3 – 2 x параллельны тогда и только тогда, когда их угловые коэффициенты совпадают, значит, угловой коэффициент касательной k = –2. С другой стороны, согласно геометрическому смыслу производной угловой коэффициент касательной k равен значению производной в точке касания: