2020-04-12
99
Пусть заряд q распределён по поверхности S с плотностью 
, различной в разных точках поверхности (рис. 13). Выделим на ней элемент ∆S, достаточно малый, для того, чтобы его можно было считать плоским, а плотность заряда на нём постоянной.
∆ S
(1)
S
(2)
S
Рис. 13. Заряженная поверхность S (её верхняя сторона считается первой, нижняя – второй)
|
|
|
Напряжённость электрического поля, созданного заряженной поверхностью S, равна
Устремим точку наблюдения 1 к середине элемента ∆S в направлении, заданном нормалью . Первый интеграл в правой части задаёт значение напряжённости на поверхности S, обозначим его
.
Второй интеграл при условии, что удаление точки наблюдения от поверхности во много раз меньше размеров элемента ∆ S, приближается к значению напряжённости около равномерно заряженной плоскости. Следовательно,
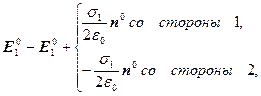
или без обозначения наблюдения
(15)
На заряженной поверхности нормальная составляющая напряжённости электрического поля 
испытывает разрыв, пропорциональный поверхностной плотности заряда:
Последнее равенство в математической физике рассматривается как теорема о скачке нормальной производной потенциала простого слоя.
