Конденсатор образован двумя неограниченными параллельными плоскостями (пластинами), одна из которых заряжена с плотностью заряда  , другая с плотностью (-
, другая с плотностью (-  ). Пусть расстояние между пластинами равно d (рис. 14).
). Пусть расстояние между пластинами равно d (рис. 14).
 X
X


 E
E
2
- 
 u12
u12
0 d 
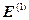 1
1  >0
>0
Рис.14. Плоский конденсатор в поперечном разрезе
Поле, созданное зарядами нижней пластины, внутри конденсатора и выше него равно 
 а ниже конденсатора
а ниже конденсатора  Поле верхней пластины внутри конденсатора и ниже него равно
Поле верхней пластины внутри конденсатора и ниже него равно  а выше конденсатора
а выше конденсатора 
Заряды обеих пластин вместе не создают электрического поля выше конденсатора  и ниже него
и ниже него  . Внутри конденсатора напряжённость электрического поля равна
. Внутри конденсатора напряжённость электрического поля равна

Напряжение между пластинами 
Если ниже конденсатора  то над конденсатором
то над конденсатором 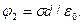
Конденсатор можно рассматривать как двойной заряженный слой. На двойном слое зарядов потенциал испытывает разрыв  . Величина
. Величина  называется плотностью двойного заряженного слоя. Если пластины конденсатора имеют ограниченные размеры, то электрическое поле распространяется за пределы конденсатора (
называется плотностью двойного заряженного слоя. Если пластины конденсатора имеют ограниченные размеры, то электрическое поле распространяется за пределы конденсатора ( и Е(2 )
и Е(2 ) 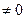 на рис. 14). Конденсатор (двойной заряженный слой) является аналогом потенциала двойного слоя в математической физике.
на рис. 14). Конденсатор (двойной заряженный слой) является аналогом потенциала двойного слоя в математической физике.
Краткое содержание четвёртой лекции. Электростатическая теорема Гаусса в дифференциальной форме  фиксирует тот факт, что источниками электрического поля являются электрические заряды, распределенные в пространстве.
фиксирует тот факт, что источниками электрического поля являются электрические заряды, распределенные в пространстве.
Теорема Гаусса в интегральной форме

позволяет рассчитывать электрические поля, которые созданы зарядами, распределёнными в пространстве симметричным образом. Симметрия поля (центральная, осевая или плоская) позволяет вынести напряженность Е за знак поверхностного интеграла при подходящем выборе поверхности S. В сложных случаях поверхностный интеграл вычислить не удаётся и найти вектор  невозможно.
невозможно.
Результаты расчёта симметричных полей используются для расчёта особенностей несобственных интегралов
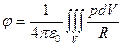 и
и 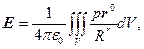
 и
и 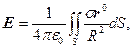
которые возникают при R  0.
0.
 2020-04-12
2020-04-12 218
218







