Поле равномерно заряженного шара

Пусть шар радиусом r₀ несёт заряд q, равномерно распределённый по объёму шара с плотностью

.

Электрическое поле обладает сферической симметрией, 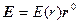. Вне шара его напряженность вычисляется так же, как в случае заряженной сферы:

соответственно  На поверхности шара

Теперь построим сферическую поверхность S так, чтобы она располагалась симметричным образом внутри заряженного шара (r<r₀). Электрический поток сквозь эту поверхность равен  где q_r  - заряд, находящийся внутри сферы радиуса r<r_{0 ,}

 

Следовательно,                                                       r<r₀.

В центре шара Е(0)=0.

Электрическое напряжение между внутренней точкой шара с координатой r и его поверхностью равно

Электрический потенциал во внутренней точке шара .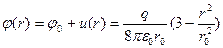

В центре шара

 

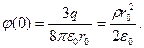
Принципиальный график потенциала и напряженности электрического поля заряженного шара в зависимости от расстояния между его центром и точкой поля показан на рис. 11.

 

                           E,

                                         

                                                                    Е

                       

                                                                                                                                    

                                                                                                                                                 

                                                                                            r                                               

 

 

                             0                                r ₀         

Рис. 11. Графики функций E(r) и (r) (c= / )

 

Этот пример имеет важное теоретическое значение. При вычислении несобственных интегралов для потенциала и напряженности электрического поля внутри заряженного тела приходится рассматривать окрестность особой точки, в которой расстояние между точкой поля и точкой источника R₂₁ равно нулю. Обычно особую точку помещают в центр шара малого радиуса . Поле в окрестности особой точки можно разделить на две составляющих: где - напряженность поля, созданного внешними по отношению к рассматриваемому шару зарядами (это непрерывная внутри шара функция),

- напряженность поля, созданного зарядом, находящимся внутри шара. Именно с и соответствующим потенциалом приходится иметь дело при вычислении несобственных интегралов. В рассмотренном здесь примере напряженность вычислена с помощью электростатической теоремы Гаусса, затем найден потенциал и показано, что в центре шара E=0 и     0 при 0. Значит, заряд, находящийся внутри шара радиуса , даёт нулевой вклад в значения интегралов

 и

когда точка поля оказывается внутри заряженного тела. Во введении(первая лекция) этому факту было дано приблизительное толкование.